Решение: Горизонтально расположенный закрытый цилиндрический сосуд длины

Условие задачи:

Горизонтально расположенный закрытый цилиндрический сосуд длины 0,6 м с гладкими стенками, разделенный на две части легким теплонепроницаемым поршнем, заполнен идеальным газом. В начальный момент объем левой части сосуда вдвое больше объема правой, а температура газа в обеих частях одинакова. На сколько переместится поршень, если температуру газа в правой части увеличить вдвое, а в левой поддерживать постоянной?

Задача №4.3.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(L=0,6\) м, \(V_1=2V_2\), \(T_1=T_2\), \(T_2^*=2T_2\), \(T_1^*=T_1\), \(\Delta l-?\)

Решение задачи:

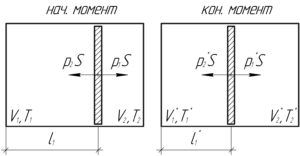Приведем рисунок для решения задачи, причем условимся писать все величины, соответствующие начальному моменту времени, писать без «звездочки», а конечному — со «звездочкой».

Так как поршень и в начальный, и в конечный момент времени будет находится в равновесии, то можно записать первый закон Ньютона и два уравнения Клапейрона-Менделеева.

\[\left\{ \begin{gathered}
{p_1}S = {p_2}S \hfill \\
{p_1}{V_1} = {\nu _1}R{T_1} \hfill \\
{p_2}{V_2} = {\nu _2}R{T_2} \hfill \\
\end{gathered} \right.\]

Из первой строки системы видно, что давления газов равны, т.е. \(p_1=p_2=p\). Зная, что по условию \(V_1=2V_2\) и \(T_1=T_2=T\), получим:

\[\left\{ \begin{gathered}
2p{V_2} = {\nu _1}RT \hfill \\
p{V_2} = {\nu _2}RT \hfill \\
\end{gathered} \right.\]

Поделив верхнее выражение на нижнее, имеем:

\[\frac{{{\nu _1}}}{{{\nu _2}}} = 2\]

Отлично, мы нашли отношение количества молей газов в левой и правой части сосуда.

Теперь повторим то же самое и для конечного момента времени, т.е. опять запишем первый закон Ньютона и два уравнения Клапейрона-Менделеева:

\[\left\{ \begin{gathered}
p_1^*S = p_2^*S \hfill \\
p_1^*V_1^* = {\nu _1}RT_1^* \hfill \\
p_2^*V_2^* = {\nu _2}RT_2^* \hfill \\
\end{gathered} \right.\]

Опять видно, что \(p_1^*=p_2^*=p^*\).

Теперь разберемся с температурами. Так как \(T_2^*=2T_2=2T\) и \(T_1^*=T_1=T\), то очевидно, что их отношение равно \(\frac{T_2^*}{T_1^*}=2\). Тогда:

\[\left\{ \begin{gathered}
{p^*}V_1^* = {\nu _1}RT \hfill \\
{p^*}V_2^* = 2{\nu _2}RT \hfill \\
\end{gathered} \right.\]

Поделим нижнее выражение на верхнее:

\[\frac{{V_2^*}}{{V_1^*}} = 2\frac{{{\nu _2}}}{{{\nu _1}}} = 2 \cdot \frac{1}{2} = 1\]

Значит поршень в конце разделит сосуд на две равные части.

Для того, чтобы узнать на сколько сместиться поршень, следует заметить такой факт:

\[\frac{L}{{{l_1}}} = \frac{V}{{{V_1}}}\]

В задаче считается, что поршень имеет нулевую толщину. В этой формуле \(V\) — это общий объем сосуда, равный \(V=V_1+V_2\), тогда:

\[\frac{L}{{{l_1}}} = \frac{V}{{{V_1}}} = \frac{{{V_1} + {V_2}}}{{{V_1}}} = 1 + \frac{{{V_2}}}{{{V_1}}} = 1 + \frac{1}{2} = \frac{3}{2} \Rightarrow {l_1} = \frac{2}{3}L\]

Проделаем такие же действия для конечного момента:

\[\frac{L}{{l_1^*}} = \frac{V}{{V_1^*}} = \frac{{V_1^* + V_2^*}}{{V_1^*}} = 1 + \frac{{V_2^*}}{{V_1^*}} = 1 + 1 = 2 \Rightarrow l_1^* = \frac{1}{2}L\]

Перемещение поршня можно найти по формуле:

\[\Delta l = {l_1} — l_1^* = \frac{2}{3}L — \frac{1}{2}L = \frac{1}{6}L\]

\[\Delta l = \frac{{0,6}}{6} = 0,1\; м \]