Условие задачи:

Электрон движется в магнитном поле с индукцией 2 мТл по винтовой линии радиусом 2 см и шагом 5 см. С какой скоростью влетел электрон в магнитное поле?

Задача №8.2.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(B=2\) мТл, \(R=2\) см, \(h=5\) см, \(\upsilon-?\)

Решение задачи:

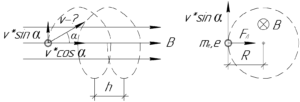Так как электрон движется в магнитном поле по винтовой линии, значит он влетел в него под некоторым углом \(\alpha\) к линиям индукции. Электрон в этом поле совершает сложное движение, состоящее из:

1. равномерного прямолинейного движения со скоростью \(\upsilon \cdot \cos \alpha\) вдоль линий индукции магнитного поля;
2. равномерного движения по окружности со скоростью \(\upsilon \cdot \sin \alpha\) в плоскостях, перпендикулярных линиям индукции магнитного поля.

Два этих движения дают в сумме движение электрона по так называемой винтовой линии.

Искомый шаг винта \(h\) — это расстояние, которое пройдет электрон вдоль линий индукции магнитного поля за время, равное периоду вращения электрона \(T\). Поэтому:

\[h = \upsilon \cos \alpha \cdot T\;\;\;\;(1)\]

Зная скорость движения электрона по окружности, можно найти период вращения электрона \(T\) по формуле:

\[T = \frac{{2\pi R}}{{\upsilon \sin \alpha }}\;\;\;\;(2)\]

Подставим (2) в (1), тогда:

\[h = \upsilon \cos \alpha \cdot \frac{{2\pi R}}{{\upsilon \sin \alpha }}\]

\[h = \frac{{2\pi R}}{{tg\alpha }}\]

\[tg\alpha = \frac{{2\pi R}}{h}\]

\[\alpha = arctg\left( {\frac{{2\pi R}}{h}} \right)\;\;\;\;(3)\]

На электрон, движущийся в магнитном поле, действует сила Лоренца \(F_Л\), которую определяет следующая формула:

\[{F_Л} = B\upsilon e\sin \alpha \;\;\;\;(4)\]

Здесь \(B\) — индукция магнитного поля, \(\upsilon\) — скорость электрона, \(e\) — модуль заряда электрона, \(\alpha\) — угол между вектором скорости и вектором магнитной индукции.

Направление действия силы Лоренца определяется правилом левой руки: если ладонь левой руки расположить так, чтобы линии магнитной индукции входили в нее, а четыре вытянутых пальца направить по направлению движения положительного заряда (или против направления отрицательного заряда, как в нашем случае), то большой палец, оставленный на 90°, покажет направление силы Лоренца. В нашем случае (при таком направлении вектора магнитной индукции) сила Лоренца направлена вправо.

Сила Лоренца \(F_Л\) сообщает электрону центростремительное ускорение \(a_ц\), поэтому из второго закона Ньютона следует, что:

\[{F_Л} = {m_e}{a_ц}\;\;\;\;(5)\]

Центростремительное ускорение \(a_ц\) можно определить через скорость, равную \(\upsilon \sin \alpha\) и радиус кривизны траектории \(R\) по формуле:

\[{a_ц} = \frac{{{\upsilon ^2}{{\sin }^2}\alpha }}{R}\;\;\;\;(6)\]

Подставим (6) в (5), тогда:

\[{F_Л} = \frac{{{m_e}{\upsilon ^2}{{\sin }^2}\alpha }}{R}\;\;\;\;(7)\]

Приравняем правые части (4) и (7):

\[B\upsilon e\sin \alpha = \frac{{{m_e}{\upsilon ^2}{{\sin }^2}\alpha }}{R}\]

Имеем:

\[Be = \frac{{{m_e}\upsilon \sin \alpha }}{R}\]

Откуда скорость электрона \(\upsilon\) равна:

\[\upsilon = \frac{{BeR}}{{{m_e}\sin \alpha }}\]

В полученную формулу подставим ранее полученное выражение (1) для нахождения угла \(\alpha\), тогда:

\[\upsilon = \frac{{BeR}}{{{m_e}\sin \left( {arctg\left( {\frac{{2\pi R}}{h}} \right)} \right)}}\]

Итак, задача решена в общем виде, осталось только посчитать численный ответ. Напомним, что масса электрона \(m_e\) равна 9,1·10^-31 кг, а его заряд \(e\) (вернее модуль заряда) равен 1,6·10^-19 Кл.

\[\upsilon = \frac{{0,002 \cdot 1,6 \cdot {{10}^{ — 19}} \cdot 0,02}}{{9,1 \cdot {{10}^{ — 31}} \cdot \sin \left( {arctg\left( {\frac{{2 \cdot 3,14 \cdot 0,02}}{{0,05}}} \right)} \right)}} = 7,57 \cdot {10^6}\;м/с = 7570\;км/с\]

Ответ: 7570 км/с.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

8.2.22 Если конденсатор с расстоянием между пластинами 1 см определенным образом
8.2.24 Заряженная частица влетает в однородное магнитное поле перпендикулярно линиям
8.2.25 Протон и альфа-частица (4He2), ускоренные одинаковой разностью потенциалов, влетают