Условие задачи:
Математический маятник совершает колебания. В положении наибольшего отклонения ускорение маятника в 10 раз больше, чем в момент прохождения равновесия. Найдите угол максимального отклонения маятника.
Задача №9.2.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\frac{a_2}{a_1}=10\), \(\alpha-?\)
Решение задачи:
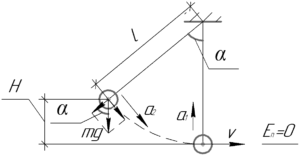Сперва будем определять ускорение маятника \(a_1\) в нижней точке траектории. Для этого нарисуем это положение маятника, при котором оно имеет максимальную скорость \(\upsilon\). Центростремительное ускорение маятника (а в этом положении маятник имеет только такое ускорение) можно найти по формуле:
\[a_1 = \frac{{{\upsilon ^2}}}{l}\]
Изначально тело находится на высоте \(H = l\left( {1 — \cos \alpha } \right)\). Из закона сохранения энергии следует (на рисунке показан уровень нуля потенциальной энергии):
\[mgH = \frac{{m{\upsilon ^2}}}{2}\]
\[mgl\left( {1 — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2}\]
\[{\upsilon ^2} = 2gl\left( {1 — \cos \alpha } \right)\;\;\;\;(2)\]
Подставим выражение (2) в (1):
\[a_1= \frac{{2gl\left( {1 — \cos \alpha } \right)}}{l}\]
\[a_1 = 2g\left( {1 — \cos \alpha } \right)\;\;\;\;(1)\]
В крайнем положении маятника на него действует некомпенсированная сила \(mg\sin \alpha\), которая будет создавать тангенциальное ускорение маятника \(a_2\), равное из второго закона Ньютона:
\[m{a_2} = mg\sin \alpha \]
\[{a_2} = g\sin \alpha \;\;\;\;(2)\]
Из условия нам известно, что в положении наибольшего отклонения ускорение маятника в 10 раз больше, чем в момент прохождения равновесия, то есть \(\frac{a_2}{a_1}=10\), поэтому учитывая (1) и (2), имеем:
\[\frac{{g\sin \alpha }}{{2g\left( {1 — \cos \alpha } \right)}} = 10\]
\[\frac{{\sin \alpha }}{{2\left( {1 — \cos \alpha } \right)}} = 10\]
\[\sin \alpha = 20 — 20\cos \alpha \]
\[\sin \alpha + 20\cos \alpha = 20\]
Разделим обе части получившегося уравнения на \(\sqrt {{1^2} + {{20}^2}} = \sqrt {401}\):
\[\frac{1}{{\sqrt {401} }}\sin \alpha + \frac{{20}}{{\sqrt {401} }}\cos \alpha = \frac{{20}}{{\sqrt {401} }}\;\;\;\;(3)\]
Тогда:
\[\left\{ \begin{gathered}
\cos \varphi = \frac{{20}}{{\sqrt {401} }} \hfill \\
\sin \varphi = \frac{1}{{\sqrt {401} }} \hfill \\
\end{gathered} \right.\]
Откуда \(\varphi = \arccos \frac{{20}}{{\sqrt {401} }}\). В таком случае уравнение (3) сводится к виду:
\[\cos \left( {\alpha — \varphi } \right) = \frac{{20}}{{\sqrt {401} }}\]
\[\alpha — \varphi = \pm \arccos \frac{{20}}{{\sqrt {401} }}\]
\[\left[ \begin{gathered}
\alpha = 0 \hfill \\
\alpha = 2\arccos \frac{{20}}{{\sqrt {401} }} \hfill \\
\end{gathered} \right.\]
Имеем два корня, один из которых, естественно, не может быть решением данной задачи.
Окончательный ответ:
\[\alpha = 2\arccos \frac{{20}}{{\sqrt {401} }} = 5,72^\circ \]
Ответ: 5,72°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
9.2.19 Первый шарик, подвешенный на нити длиной 1 м, отклонили от положения равновесия
9.2.21 Кубик совершает малые колебания в вертикальной плоскости, двигаясь без трения
9.2.22 Небольшой металлический шарик массой 10 г, подвешенный на нити длиной 0,1 м
очень интересно. но тогда уберите из егэ вопрос в задаче 18 номер один в пособии демидовой 2024
по решению задачи Вы пытаетесь сравнить
тангенциальное ускорение верхней точки
с
частью нормального ускорения нижней точки…
В верхней точке ускорение не может быть больше чем в нижней.
Даже из тех соображений, что натяжение нити в нижней точке больше чем в верхней.
(опечатка)
В нижней точке
a = g + V^2 / L
В нижней точке
a = m g + m V^2 / L
в верхней точке
a_n = m g cos(alpha)
a_tau = m g sin(alpha)
полное ускорение в верхней точке
a = g
1) о каких ускорениях идет речь в задаче?
2) что надо сравнивать: полные ускорения(их модули) или тангенциальные? по условию задачи это совсем не ясно (или ясно не совсем)
3) ИТОГО: задача решена неверно!
Последнее слово оставим за истиной.
В ИСО закон независимого действия сил утверждает: ускорение от одновременного действия всех сил является векторной суммой ускорений, созданных отдельными силами. По линии отвеса на него действуют две силы: тяжести – вниз, и натяжения нити – вверх. Над точкой подвеса маятник не смещается по вертикали. Когда результирующая сил, действующих на тело, равна нулю, оно остается в состоянии покоя или продолжает движение с постоянной скоростью (первый закон Ньютона). Математически этот закон записывается в виде
F = 0, а = 0, v = const.
В самой низкой точке траектории суммарный вектор ускорений равен нулю, маятник движется по инерции и с постоянным вектором скорости, касательным к траектории.
«Последнее слово оставим за истиной.» — Я только за, считаю из спора выносит больше выгоды тот, кто был не прав.
Вы, уважаемый автор, защищаете больше свою честь, нежели истину.
Фрагмент Вашего текста: » … откуда взялось центробежное, если его добавляют лишь в неинерциальных системах отсчета». А вы обрежьте нить маятника во время движения, когда он займет вертикальное положение в системе отсчета нашей Земли. Убедитесь, что лишенное связи тело будет смещаться в двух взаимно перпендикулярных направлениях: горизонтальном и вертикальном. Эту закономерность использовали древние, когда бросали камни пращой. Другой пример: закрепите груз маятника на пружине и понаблюдайте за ее растяжением на пути от максимального угла отклонения до нуля.
Насчет тангенциального ускорения. Его создает сила веса при отклонении маятника, которую мы проектируем на ось (Х) параллельную горизонтальной плоскости. Маятник набирает горизонтальную скорость под действием горизонтальной силы и положительного ускорения. В нижней точке вектор горизонтальный скорости перпендикулярен линии отвеса. Проекция горизонтальной силы на ось Х во время движения остается постоянной, до того момента пока маятник не прошел самую низкую точку. После чего возникает возвращающая сила, которая противодействует и замедляет скорость маятника. Над точкой подвеса располагается самая низкая точка траектории. Когда ускорение переходит точку минимума, оно меняет свой знак. В самой точке скорость не растет и не уменьшается, проекция скорости центра масс на ось Х в данной месте остается величиной постоянной. С противоположных сторон от точки устойчивого равновесия маятника, т. е. вблизи ее окрестности, векторы тангенциального ускорения (положительного и отрицательного) располагаются под углом, который мало отличается от 90°. Поэтому мы вправе заявлять, что на маятник, который приближается к линии отвеса (или удаляется от нее), действуют горизонтальная сила и горизонтальное ускорение, перпендикулярное к линии натяжения нити.
Наличие центростремительного ускорения говорит о том, что связь удерживает тело от вертикального смещения, когда маятник находится над точкой подвеса. Вы же не станете опровергать, что реакция связи равна весу подвешенного груза. Представим действие вертикальных сил на маятник в точке устойчивого равновесия через равнодействующую
R = Р + Т = 0
или
Р = – Т, mg = – ma, g = – a.
Подводя итоги, констатируем: векторы центробежного и центростремительного ускорения над точкой подвеса равны и противоположно направлены, т. к. имеют разные знаки.
Думается, что дополнительных доказательств по этому вопросу больше не требуется. Надо понимать физику явления, а не опираться на интерпретацию ученых людей (даже известных).
«Вы, уважаемый автор, защищаете больше свою честь, нежели истину.» — Я истину защищаю, как свою честь!
«А вы обрежьте нить маятника во время движения, когда он займет вертикальное положение в системе отсчета нашей Земли. Убедитесь, что лишенное связи тело будет смещаться в двух взаимно перпендикулярных направлениях: горизонтальном и вертикальном.» — Да, в горизонтальном оно будет двигаться равномерно по инерции, а в вертикальном — ускоренно вниз из-за действия силы тяжести.
«Проекция горизонтальной силы на ось Х во время движения остается постоянной, до того момента пока маятник не прошел самую низкую точку.» — Нет. При гармонических колебаниях маятника справедливо \(a = — A{\omega}^2 \cos (\omega t)\), значит сила не может быть постоянной.
«В самой точке скорость не растет и не уменьшается, проекция скорости центра масс на ось Х в данной месте остается величиной постоянной.» — Вооооот. Наконец-то Вы сами признали, что в нижней точке траектории тангенциальное ускорение равно нулю. Скорость не изменяется по величине, значит тангенциальное ускорение равно нулю!
«Поэтому мы вправе заявлять, что на маятник, который приближается к линии отвеса (или удаляется от нее), действуют горизонтальная сила и горизонтальное ускорение, перпендикулярное к линии натяжения нити.» — При ближении к точке сила и ускорение есть, а в самой точке — нет!
«Вы же не станете опровергать, что реакция связи равна весу подвешенного груза.» — Сила тяжести не равна силе натяжения нити, а поэтому и реакции опоры в точке подвеса. Все из-за наличия центростремительного ускорения (которое у Вас равно какому-то центробежному).
«Думается, что дополнительных доказательств по этому вопросу больше не требуется. Надо понимать физику явления, а не опираться на интерпретацию ученых людей (даже известных).» — Как не требуется то?! Просим пояснений!
Я решал задачу исходя из второго закона Ньютона и считаю, что решение верное. Читая Ваши комментарии, создалось впечатление, что Вы плохо понимаете, что такое ускорение, очень плохо разбираетесь в их видах (тангенциальном и нормальном), откуда-то у Вас появилось центробежное ускорение (не, ну можно и так решать, зачем тогда Вам центростремительное ускорение — мне это все так и осталось загадкой). Дальше продолжать не буду. Пусть каждый останется при своем мнении. Один вопрос: Вы сомневаетесь в законах классической физики, описанных в учебниках физики за 10-11 классы?
На всякое тело, находящегося вблизи земной поверхности, действует силовое поле, направленное вертикально вниз – это сила тяжести. Система совершает колебательные движения в однородном поле тяжести, для которого g = const. Из закона сохранения энергии следует, что кинетическая энергия груза в нижней точке траектории равна убыли его потенциальной энергии в поле тяготения Земли. При колебании маятника, когда он достигает крайнего отклонения, вся его кинетическая энергия превращается в потенциальную
П = m·g·h, h = L – Lсоsθ,
где L – это радиус окружности, по которой движется груз, θ – угол отклонения.
Достигнув самой низкой точки траектории, маятник завершает превращение потенциальной энергии в кинетическую
К = m·v·v/2.
Учитывая, что при опускании с высоты h потенциальная энергия перешла в кинетическую, получим:
К = П, v·v = 2g·L(1 – соsθ).
Скорость груза определится извлечением квадратного корня из левой и правой частей последнего выражения.
Координаты центра масс и конфигурация сил, действующих на маятник, измененяются во время движения. Плоское движение точки по дуге окружности можно разложить на горизонтальную и вертикальную составляющие. Создание малого перемещения dх невозможно без действия горизонтальной силы и ускорения. Когда х = 0, горизонтальное ускорение и горизонтальная сила равны нулю. При малых углах отклонения горизонтальная сила и горизонтальное ускорение маятника пропорциональны величине смещения (х) от линии отвеса. Движение маятника над точкой отвеса – одна из возможных точек траектории. Вектор скорости равен первой производной от радиуса-вектора точки по времени и направлен в сторону движения маятника по касательной к траектории. Маятник движется над точкой минимальной высоты с постоянной горизонтальной скоростью, т. к. касательная параллельна оси ОХ, что соответствует dv/dt = 0. Векторы тангенциальных ускорений вблизи окрестности точки устойчивого равновесия располагается параллельно оси ОХ.
Повторим: над точкой подвеса на маятник действуют равные и противоположно направленные силы – это сила натяжения нити и сила тяжести. Их равнодействующая равна нулю. Значит, результирующая вертикальных ускорений в этой точке равна нулю.
Не все так просто с гармоническими колебаниями маятника, как это описывают учебники. Не буду поднимать дискуссию, но согласитесь: один вариант – опускаться в направлении силы тяжести, другой – подниматься, встречая ее противодействие. Чтобы маятник долго качался, нужны смещения перпендикулярные вектору g. Длинная нить подвеса и малые углы отклонений создают, приближенно, указанные условия и видимость соблюдения некоторой закономерности.
Конечно, никто не отрицает физические законы. Вопрос в том, что их не всегда трактуют верно. Спасибо за участие в разговоре.
Я устал спорить, надеюсь нас позже рассудит кто-то третий.
Тем не менее, я остался не согласен с некоторыми Вашими суждениями, перечислять их все я не буду. Вот это откровенная необоснованная неправда — «Над точкой подвеса на маятник действуют равные и противоположно направленные силы – это сила натяжения нити и сила тяжести.» Такого не может быть, поскольку маятник движется по криволинейной траектории, что говорит о наличии центростремительного ускорения. Или Вы рассуждаете о каком-то случае, в котором маятник подвешен на очень длинной нити. Мне все это осталось непонятным.
Думаю, что Ваши комментарии могут быть правдивы, но в неведомом для меня случае. К данной задаче их применять нельзя (да и можно ли применять к любой другой задаче), поскольку они противоречат условию — ускорения в крайней и нижней точках должны отличаться в 10 раз.
Тем не менее, спасибо за потраченное время и внимание данной задаче.
Задача №9.2.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Вектора силы тяжести и натяжения нити, занимают вертикальное положение, когда маятник имеет максимальную скорость. По линии отвеса действуют центростремительное и центробежное ускорения. Поскольку они равны и противоположно направлены, то векторная сумма этих ускорений равна нулю. Поэтому в данной точке действует только тангенциальное ускорение. Вектор силы, соответствующий этому ускорению, направлен по касательной к линии траектории маятника (горизонтально).
Изложенное выше решение ошибочно предполагает, что неуравновешенное центростремительное ускорение поднимает в этой точке массивное тело вверх. Поэтому следует считать приведенный ответ не верным.
Разберу Ваш комментарий по предложениям.
«Вектора силы тяжести и натяжения нити, занимают вертикальное положение, когда маятник имеет максимальную скорость.» — Согласен, в нижней точке траектории такое имеет место, все верно.
«По линии отвеса действуют центростремительное и центробежное ускорения.» — А вот здесь я уже не согласен. Да, центростремительное ускорение есть, но откуда взялось центробежное, если его добавляют лишь в неинерциальных системах отсчета для учета этой самой инерциальности. Где у меня в решении написано про неинерциальность? Я все решаю в инерциальной системе отсчета Земли, об этом можно даже не писать, поскольку это система отсчета по умолчанию.
«Поскольку они равны и противоположно направлены, то векторная сумма этих ускорений равна нулю.» — Соответственно здесь тоже неверно.
«Поэтому в данной точке действует только тангенциальное ускорение. Вектор силы, соответствующий этому ускорению, направлен по касательной к линии траектории маятника (горизонтально).» — Это предложения просто ужасны, они показывают, что Вы не понимаете второй закон Ньютона. Если у Вас в касательном направлении нет сил, то откуда взяться ускорению?!
«Изложенное выше решение ошибочно предполагает, что неуравновешенное центростремительное ускорение поднимает в этой точке массивное тело вверх. Поэтому следует считать приведенный ответ не верным.» — Но так и есть! Наличие центростремительного ускорения говорит о том, что тело движется по криволинейной траектории и имеет скорость, отличную от нуля. Учитывая то, что на тело наложена связь (нить), понятно, что тело будет подниматься по круговой траектории вверх.