Условие задачи:
За первую секунду равноускоренного движения тело проходит путь 1 м, а за вторую — 2 м. Определить путь, пройденный телом за первые три секунды движения.
Задача №1.3.31 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=1\) м, \(S_2=2\) м, \(S-?\)
Решение задачи:
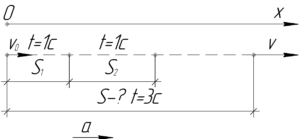 Заметим, что в условии не сказано, была ли у тела начальная скорость или нет. Чтобы решить задачу необходимо будет определить эту начальную скорость \(\upsilon_0\) и ускорение \(a\).
Заметим, что в условии не сказано, была ли у тела начальная скорость или нет. Чтобы решить задачу необходимо будет определить эту начальную скорость \(\upsilon_0\) и ускорение \(a\).
Давайте поработаем с имеющимися данными. Путь за первую секунду, очевидно, равен пути за \(t_1=1\) секунду. А вот путь за вторую секунду необходимо находить как разность пути за \(t_2=2\) секунды и \(t_1=1\) секунду. Запишем сказанное на математическом языке.
\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_1} + \frac{{at_1^2}}{2} \hfill \\
{S_2} = \left( {{\upsilon _0}{t_2} + \frac{{at_2^2}}{2}} \right) — \left( {{\upsilon _0}{t_1} + \frac{{at_1^2}}{2}} \right) \hfill \\
\end{gathered} \right.\]
Или, что является тем же самым:
\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_1} + \frac{{at_1^2}}{2} \hfill \\
{S_2} = {\upsilon _0}\left( {{t_2} — {t_1}} \right) + \frac{{a\left( {t_2^2 — t_1^2} \right)}}{2} \hfill \\
\end{gathered} \right.\]
В этой системе два уравнения и два неизвестных, значит она (система) может быть решена. Не будем пытаться ее решить в общем виде, поэтому подставим известные нам численные данные.
\[\left\{ \begin{gathered}
1 = {\upsilon _0} + 0,5a \hfill \\
2 = {\upsilon _0} + 1,5a \hfill \\
\end{gathered} \right.\]
Отняв из второго уравнения первое, получим:
\[a = 1\; м/с^2\]
Если подставить полученное значение ускорения в первое уравнение получим:
\[{\upsilon _0} = 0,5\; м/с\]
Теперь, чтобы узнать путь, пройденный телом за три секунды, необходимо записать уравнение движения тела.
\[S = {\upsilon _0}t + \frac{{a{t^2}}}{2}\]
В итоге ответ равен:
\[S = 0,5 \cdot 3 + \frac{{1 \cdot {3^2}}}{2} = 6\; м\]
Ответ: 6 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.3.30 Автомобиль, двигаясь равноускоренно, прошел два смежных участка пути
1.3.32 За седьмую секунду равноускоренного движения модуль вектора скорости
1.3.33 К концу первой секунды равнозамедленного движения модуль скорости тела
От куда взялось 0.5 и 1.5?
Если Вы в эту систему:\[\left\{ \begin{gathered}
{S_1} = {\upsilon _0}{t_1} + \frac{{at_1^2}}{2} \hfill \\
{S_2} = {\upsilon _0}\left( {{t_2} — {t_1}} \right) + \frac{{a\left( {t_2^2 — t_1^2} \right)}}{2} \hfill \\
\end{gathered} \right.\]подставите численные данные, а конкретно \(S_1=1\) м, \(S_2=2\) м, \(t_1=1\) с и \(t_2=2\) с, то получите уже такую систему:\[\left\{ \begin{gathered}
1 = {\upsilon _0} + 0,5a \hfill \\
2 = {\upsilon _0} + 1,5a \hfill \\
\end{gathered} \right.\]
А может просто нужно с1 прибавить с2 и получается с3
Ну если Вы к 1 с прибавите 2 с, то не получите 6 с, верно?
нельзя, потому что движение равноускоренное, то есть скорость, а соответственно и пройденный телом путь, увеличивается
Я что то не понял)))))))))))))))))))))
Это нормально) У вас всегда есть возможность перечитать решение задачи, чтобы понять её