Условие задачи:
Тело брошено с высоты 2 м горизонтально так, что к поверхности земли оно подлетает под углом 45° к горизонту. Какое расстояние по горизонтали пролетит тело?
Задача №1.5.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=2\) м, \(\alpha=45^\circ\), \(S-?\)
Решение задачи:
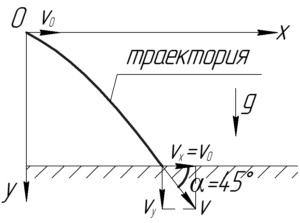Скорость тела при падении всегда можно разложить на составляющие. Если тело подлетает под углом 45° к горизонту, значит вертикальная и горизонтальная составляющие этой скорости равны между собой, т.к. в прямоугольном треугольнике с углом 45° катеты равны между собой. Это можно было доказать и другим путем, например, расписав тангенс данного угла.
\[{\text{tg}}\,\alpha = \frac{{{\upsilon _y}}}{{{\upsilon _x}}}\]
\[{\text{tg}}\,45^\circ = 1 \Rightarrow {\upsilon _y} = {\upsilon _x}\,\,\,(1)\]
Запишем уравнения скорости, спроецированные на оси координат.
\[\left\{ \begin{gathered}
ox:{\upsilon _x} = {\upsilon _0}\,\,\,(2) \hfill \\
oy:{\upsilon _y} = gt\,\,\,(3) \hfill \\
\end{gathered} \right.\]
Исходя из (1) следует, что:
\[{\upsilon _0} = gt\]
Также нам необходимы уравнения движения по осям координат:
\[\left\{ \begin{gathered}
ox:x = {\upsilon _0}t\,\,\,\,\,\,(4) \hfill \\
oy:y = \frac{{g{t^2}}}{2}\,\,\,(5) \hfill \\
\end{gathered} \right.\]
Если в этих уравнениях \(t\) — это продолжительность падения тела, то верно, что:
\[\left\{ \begin{gathered}
S = {\upsilon _0}t\,\,\,\,\,\,(6) \hfill \\
H = \frac{{g{t^2}}}{2}\,\,\,(7) \hfill \\
\end{gathered} \right.\]
Используя формулу (6) и зная, что \({\upsilon _0} = gt\) и \(H = \frac{{g{t^2}}}{2}\), следует:
\[S = {\upsilon _0}t = g{t^2} = 2H\]
\[S = 2 \cdot 2 = 4\; м \]
Ответ: 4 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.5.8 Понижение траектории снаряда, выпущенного из горизонтально расположенного
1.5.10 Спортсменка, стоящая на вышке, бросает мяч с горизонтальной скоростью
1.5.11 Тело брошено горизонтально с высоты h=20 м. Траектория его движения
а что делать если в начале кинули не горизонтально, а например под углом, например 60, что тогда делать
Уравнения 2-5 будут другими, нужно их записать, а дальше уже смотреть, что Вам нужно найти в задаче и что дано в условии
в последнем уравнении 2h не равно на s как бы s = h если я не понимаю здесь что то можете обьяснить подробнее на этом задаче уже сижу 20 мин и не могу понять
Мы получили, что \({\upsilon _0} = gt\).
Далее получили, что \(S = {\upsilon _0}t\), учитывая вышенаписанное, получим \(S = g{t^2}\).
Также мы знаем, что \(H = \frac{{g{t^2}}}{2}\). Вот отсюда и понятно, что \(S = 2H\).
А если угол 60
У Вас не получится равенства (1), но Вы получите это:
v_y=v_x*tg a
Потом у Вас должно получится следующее:
v0=(g*t)/tg a
Далее нужно выполнить те же подстановки, что описаны выше.
Как видите, задача не становится сложнее.
а нельзя решить формулой H=V^2sin^2a/2g и L=V^2sin2a/g
???
Я лично считаю, что физика — это не тот предмет, где нужно просто применить заученную формулу. Изучение физики принесёт пользу лишь в том случае, когда Вы можете обосновать ответ, т.е. запишите некоторые законы (в данном случае — уравнения движения и скоростей на оси координат) и далее из них получите ответ. Навык обосновывания своих решений Вам очень пригодится в жизни!
Поэтому, если Вы получили эти формулы самостоятельно путем логических рассуждений, то я оставлю за Вами ответ на вопрос «Можно ли решать задачу такими формулами». А если не сами — то лучше воспользуйтесь решением, приведённым выше.