Условие задачи:

Струя воды бьет под углом 32° к горизонту. На расстоянии в 12 м она падает. Площадь отверстия шланга 1 см². Сколько воды подает шланг за минуту?

Задача №1.6.21 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=32^\circ\), \(L=12\) м, \(S=1\) см², \(t=1\) мин, \(V-?\)

Решение задачи:

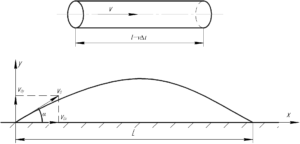Для решения этой интересной задачи нужно взглянуть на верхнюю часть рисунка-пояснения, приведенного справа. За каждый малый отрезок времени \(\Delta t\) из шланга вылетает объем воды \(\Delta V\), т.е.:

\[\Delta V = S \cdot\Delta l = S \cdot v_0 \cdot \Delta t\]

Совершенно очевидно, что объем воды \(V\), подаваемой шлангом за минуту, можно найти по следующей формуле:

\[V = S \cdot l = S \cdot v_0 \cdot t\]

Чтобы решить эту задачу, нужно понять, что каждую секунду из шланга выходит один и тот же объем воды, что в принципе и видно из формул выше. Теперь, для получения ответа нам не известна лишь начальная скорость струи. Обращаясь к нижней части рисунка-пояснения, запишем уравнения движения в проекциях на оси \(x\) и \(y\).

\[\left\{ \begin{gathered}
ox:x = {v_0}\cos \alpha \cdot t\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(1) \hfill \\
oy:y = {v_0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2}\,\,\,\,(2) \hfill \\
\end{gathered} \right.\]

В точке падения струи на землю, координата части струи, упавшей на землю, равна нулю, поэтому приравняем уравнение (2) к нулю.

\[y = 0 \Rightarrow {v_0}\sin \alpha  \cdot t — \frac{{g{t^2}}}{2} = 0\]

Решая уравнение, получаем 2 корня, первый из которых нам не нужен, поскольку он указывает на начальный момент времени.

\[\left[ \begin{gathered}
t = 0 \hfill \\
t = \frac{{2{v_0}\sin \alpha }}{g} \hfill \\
\end{gathered} \right.\]

Подставим второй корень в уравнение (1) и получим уравнение для определения дальности полета, откуда выразим \(v_0\):

\[L = \frac{{v_0^2\sin 2\alpha }}{g} \Rightarrow {v_0} = \sqrt {\frac{{Lg}}{{\sin 2\alpha }}} \]

В заключении, подставим полученную формулу в приведенную выше формулу для определения \(V\):

\[V = \sqrt {\frac{{Lg}}{{\sin 2\alpha }}} St\]

Подставим все полученные величины в СИ и получим ответ:

\[V = \sqrt {\frac{{12 \cdot 10}}{{\sin \left( {2 \cdot 32^\circ } \right)}}}  \cdot {10^{ — 4}} \cdot 60 = 0,069\; м^3\].

Ответ: 0,069 м³.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Если Вам понравилась задача и ее решение, то Вы можете поделитесь ею с друзьями с помощью этих кнопок.

Смотрите также задачи:

1.6.20 С вершины холма бросают камень с начальной скоростью
1.6.22 Тело брошено под углом 60 к горизонту с начальной скоростью
1.7.1 Определить скорость относительно берега реки лодки, идущей перпендикулярно