Условие задачи:
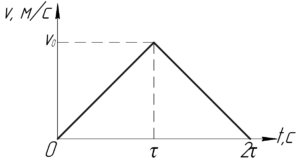Поезд начинает двигаться по прямой, параллельной оси \(x\). Зависимость скорости поезда от времени показана на рисунке (показан справа). За 20 мин поезд прошел 18 км. Найти ускорение поезда в промежутке \(\left[ {0,\tau } \right]\), где \(\tau=10\) мин.
Задача №1.1.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=18\) км, \(\tau=10\) мин, \(a-?\)
Решение задачи:
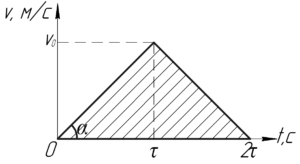Начнем решение с конца. Поезд в промежутке \(\left[ {0,\tau } \right]\) движется равноускоренно (это видно по графику), и его ускорение можно найти как тангенс угла наклона графика скорости:
\[a = tg\alpha = \frac{{{\upsilon _0}}}{\tau }\;\;\;\;(1)\]
Так как нам известно сколько прошел поезд за все время, то найдем из выражения для пути неизвестную максимальную скорость \(\upsilon _0\). Нам известно, что площадь фигуры под графиком скорости численно равно пройденному пути. Такой фигурой у нас является треугольник, его площадь можно найти как полупроизведение основания на высоту, то есть:
\[S = \frac{1}{2}2\tau \cdot {\upsilon _0} = {\upsilon _0}\tau \Rightarrow {\upsilon _0} = \frac{S}{\tau }\]
Подставим \(\upsilon _0\) в формулу (1):
\[a = \frac{S}{{{\tau ^2}}}\]
Осталось подставить исходные данные в системе СИ, т.е. путь в метрах (м), а время – в секундах (с).
\[a = \frac{{18000}}{{{{600}^2}}} = 0,05\; м/с^2 = 5\; см/с^2\]
Ответ: 5 см/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.1.4 График зависимости скорости тела от времени имеет вид полуокружности
1.1.6 Какова скорость транспортера, если за 5 с он перемещается на 10 м?
1.1.7 Расстояние между двумя городами автомашина проехала со скоростью 60 км/ч
ееееееее правильно решил
“Найти ускорение поезда в промежутке [0,τ]”,- т.е. мы находим ускорение только в первой половине пути, в таком случае я не понимаю, почему в решении используется весь путь поезда, объясните, пожалуйста. У меня вышло 0.025 м/с^2
V0 = 0 м/c
t = 600 c.
S = 18000 м
V = S/t
V = 18000/600 = 30 м/c
По графику видно, что движение равноускоренное => a = (V-V0)/t = 30/600 = 0.05 м/c^2 = 5 см/с^2
Решение верное, но предварительно нужно доказать, что v=S/t, поскольку это формула для определения скорости при равномерном движении, а по графику видно, что движение равнопеременное (сначала равноускоренное, потом равнозамедленное)
а можно решить через 1 формулу: x=a*t^2/2 => a = 2x/t^2
a = 2*9000м/600^2 = 0,05м/с
Решение правильное, но нужно предварительно нужно доказать, что за время \(\tau\) поезд пройдет путь \(\frac{S}{2}\).
У меня, глядя на Ваше решение, сразу возникает вопрос, откуда Вы взяли 9 км?
высота, в треугольнике по рисунку еще и медиана, т.е треугольник равнобедренный следовательно площади половинок равны- пути равны
Вот теперь верю
А какое определение тангенса угла наклона? Почему скорость делим на время? Не понял этот момент
На графике указан угол \(\alpha\), тангенс этого угла можно найти с помощью графика из прямоугольного треугольника, где противолежащим катетом будет \(\upsilon_0\), а прилежащим – \(\tau\).
Когда сам считал, получился другой ответ.. Мы же делим 18000 на 360000,почему 0,05?
\[\frac{{18000}}{{360000}} = \frac{{18}}{{360}} = \frac{1}{{20}} = 0,05\]
а где взять сам задачник?
кто-то выкладывал в группе вк, поищите в обсуждениях
в откуда 600??
Чтобы получить ответ в единицах СИ, то есть в м/с^2, численные величины в формулу также нужно подставлять, выраженные в единицах системы СИ. Поэтому время мы подставили в секундах, 10 мин = 600 с.
а если это график пути, то можно найти скорость через тангенс угла наклона?
Да, можно
я не понимаю зачем нужно было выводить формулу и приплетать сюда тангенс ,если решили по простой формуле путь разделили на время ,или я что то не понимаю,можете пояснить
Движение поезда – ускоренное, так как график скорости от времени выглядит в виде прямой, поэтому чтобы найти ускорение, нам нужно было “приплетать” тангенс.
Формула v=S/t работает только для равномерного движения, ее тут использовать нельзя.
А вот тут уже можно использовать мой пример: найдем минимальную скорость в данном промежутке, по графику она равна нулю, ну а максимальная скорость v0.
максимальную скорость тоже можно найти по моему примеру: 18000/2= 9000м( половина пути илии же нужный промежуток) 9000м за 10 минут, то есть средняя скорость 9000/600= 15
с.с(средняя скорость)= ((минимальная) + v0(максимальная))/2
15= (0+макс)/2 –> 30=0 + макс
макс. скрость(v0)=30
а=3000см/с / 600с = 5 см/с2
просто скажите, мой способ решения таких задач хоть и, не знаю, предельно прост и сильно упрошен( так решают задачи в 4-ом классе ) он ведь верный? Учителя в школе твердят что это не правильно(
Вы получаете верный ответ, ваши действия вполне логичны, но задачи в физике принято решать без промежуточных вычислений. Нужно стремиться к решению, предложенному на этой странице.
от куда 600 в квадрате взялось??
В формулу подставляем время в секундах, при этом 10 мин = 600 с
А Вы можете пояснить, почему ускорение мы находим, как tga? Не могу понять, почему))
В математике есть понятие линейной функции:
\[y = kx + b\]
Если график функции проходит через начало координат, то:
\[\begin{gathered}
b = 0 \hfill \\
y = kx \hfill \\
\end{gathered} \]
Видно, что коэффициент k равен:
\[k = \frac{y}{x}\]
На графике видно, что это отношение равно тангенсу угла наклона прямой к положительному направлению оси ox.
Теперь проводите аналогию – скорость у нас меняется линейно, в начальный момент скорость равна нулю. Поэтому справедливо для отрезка времени от 0 до tau записать:
\[\upsilon = at\]
Значит по аналогии ускорение a равно тангенсу угла наклона alpha.
Не уверен,но кажется у вас ошибка в задаче.ускорение рассчитывается по формуле a=S/t^2 и делить это на 2.Зная,что расстояние равно S=at^2/2
Нет ошибки, все предельно ясно написано в решении)
Я нахожу ускорение через скорость v0. А саму скорость v0 нахожу из пути S, который равен площади фигуры по графиком изменения скорости.
Физика – это не применение заученных формул)
спасибо,буду знать!!!))
Не делить, а умножить)
Верное замечание, спасибо