Условие задачи:
Камень упал в шахту. Определить глубину шахты, если звук от падения камня был слышен наверху через 6 с. Скорость звука 330 м/с.
Задача №1.4.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(t=6\) с, \(\upsilon_{зв}=330\) м/с, \(h-?\)
Решение задачи:
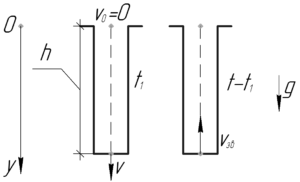Описываемый в условии задачи процесс происходит следующим образом. Камень бросают без начальной скорости в шахту, он будет двигаться равноускоренно и через время \(t_1\) достигнет дна шахты, затем звук удара камня о дно устремится в разные стороны и достигнет человека, бросившего камень. Звук, кстати, распространяется равномерно – это есть механическая волна. В этой задаче звук будет двигаться до человека время, равное \(t-t_1\).
То есть время 6 секунд, данное в условии – это время от момента броска камня до момента достижения звуком человека. Понятно, что и камень, и звук пройдут одинаковое расстояние, поэтому верно записать следующее.
\[\frac{{gt_1^2}}{2} = {\upsilon _{зв}}\left( {t – {t_1}} \right)\]
Раскроем скобки в равенстве, перенесем все слагаемые в одну сторону, подставим численные данные и решим квадратное уравнение.
\[\frac{{gt_1^2}}{2} + {\upsilon _{зв}}{t_1} – {\upsilon _{зв}}t = 0\]
\[5t_1^2 + 330{t_1} – 1980 = 0\]
\[t_1^2 + 66{t_1} – 396 = 0\]
Вычислим дискриминант \(D\).
\[D = 4356 + 4 \cdot 396 = 5940\]
\[{t_1} = \frac{{ – 66 \pm \sqrt {5940} }}{2} = – 33 \pm \sqrt {1485} \]
\[\left[ \begin{gathered}
{t_1} = 5,54 \; с \hfill \\
{t_1} = – 71,54 \; с \hfill \\
\end{gathered} \right.\]
Время не может быть отрицательным, поэтому отбрасываем корень со знаком “минус”.
Но мы еще не нашли ответ. В задаче нужно узнать глубину шахты \(h\), а ее можно посчитать по нижеприведенной формуле.
\[h = \frac{{gt_1^2}}{2}\]
\[h = \frac{{10 \cdot {{5,54}^2}}}{2} = 153,46 \; м \approx 153\; м \]
Ответ: 153 м.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.4.18 Из точки A вертикально вверх брошено тело с начальной скоростью 10 м/с
1.4.20 Мяч брошен с земли вертикально вверх. На высоте 10 м он побывал два раза
1.4.21 Тело бросают вертикально вверх. Наблюдатель замечает промежуток времени
такое чувство будто сложность задач именно в условии…
такое чувство будто сложность задач именно в условии…
Спасибо вам большое, очень помогли мне понять суть этой задачи!Теперь, я смог ее решить самостоятельно благодаря вам!
А разве когда мы всё приравниваем к нулю, мы не домножаем на 2, чтобы избавиться от двойки на которую делим gt
Нет, я в квадратное уравнение\[\frac{{gt_1^2}}{2} + {\upsilon _{зв}}{t_1} – {\upsilon _{зв}}t = 0\]подставил численные значения \(g\), \(\upsilon_{зв}\) и \(t\) и получил уже уравнение:\[5t_1^2 + 330{t_1} – 1980 = 0\]
если время t до того как мы услышим звук, время t1 это время от момента касания камня до того как мы услышим звук, то t-t1 – время падения камня до касания дна.
g(t-t1)^2/2=vt1
но при решении этого уравнения два корня положительные.. где ошибка?
Нужно проверить условие \({t_1} < t\), вероятно один корень не будет удовлетворять этому условию.
А почему время t-t1, можете поподробнее объяснить почему мы вычитаем
В решении \(t\) – это время от момента начала падения камня до того момента, когда звук от падения камня будет слышен у поверхности земли, \(t_1\) – время падения камня в шахте. По логике понятно, что время \(\left( {t – {t_1}} \right)\) звук от падения камня будет двигаться в шахте до поверхности. Ничего сложного нет.
Как из √5940 получился √1485?
\[\sqrt {5940} = \sqrt {4 \cdot 1485} = 2\sqrt {1485} \]Далее числитель делится почленно на знаменатель
Довольно неоднозначное условие. Лучше дописать, что через 6 секунд после того, как бросили камень (т.к я подумал, что после падения камня звук слышен через 6 секунд)
Условия размещенных задач я никогда не правлю и оставляю их без изменений (то есть авторскими).
Да, условие вообще неоднозначное, также вызывает сомнение то, существуют ли вообще колодцы такой глубины?
Кстати, если решать так, как Вы подумали, то задача решается чересчур просто.
не поняла с дискриминантом. это же неправильные числа, и можно сделать так же, но что бы вместо 330 было 340?
Что такое неправильные числа?
Можно, если Вам указано в условии.
Подскажите, пожалуйста, откуда взялось, что g=10?
g – это ускорение свободного падения, для расчётов можно принимать g=10 м/с2 (так, например, и делается на ЕГЭ)
можно и так h=g*t^2/2=9.8*36/2=176 проверяем;=> tпадения=kopen2*h/g=koren352/9.8=koren35.9=5.9916…….
Неправильное решение.
Перечитайте условие и ознакомьтесь с решением.