Решение: В трёх вершинах квадрата со стороной 1 м находятся положительные точечные заряды

Условие задачи:

В трёх вершинах квадрата со стороной 1 м находятся положительные точечные заряды 0,1 мкКл каждый. Определить модуль вектора напряженности электрического поля в центре квадрата.

Задача №6.2.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(a=1\) м, \(q=0,1\) мкКл, \(E-?\)

Решение задачи:

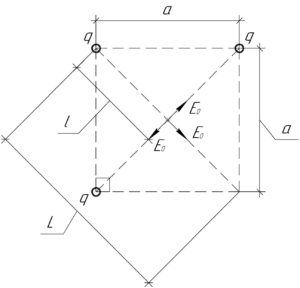Длину диагонали квадрата \(L\), которую можно найти по теореме Пифагора:

\[L = \sqrt {{a^2} + {a^2}} = \sqrt 2 a\]

Центр квадрата – это точка пересечения его диагоналей. Пусть \(l\) – расстояние от каждой вершины до центра квадрата, это расстояние равно половине длины диагонали квадрата \(L\), поэтому:

\[l = \frac{L}{2} = \frac{{\sqrt 2 a}}{2}\;\;\;\;(1)\]

Так как все заряды одинаковые по величине и находятся на одинаковом расстоянии от центра квадрата, то в этой точке каждый из них будет создавать электрическое поле напряженностью \(E_0\), модуль которой найдём следующим образом:

\[{E_0} = \frac{{kq}}{{{l^2}}}\]

Здесь \(k\) – коэффициент пропорциональности, равный 9·10⁹ Н·м²/Кл².

Учитывая (1), имеем:

\[{E_0} = \frac{{2kq}}{{{a^2}}}\]

Вектор напряженности результирующего поля \(\overrightarrow E\) равен геометрической сумме всех векторов \(\overrightarrow {{E_0}}\). Так как два из них лежат на одной прямой и направлены противоположно, то их сумма равна нулевому вектору (смотрите схему). Поэтому:

\[E = {E_0}\]

\[E = \frac{{2kq}}{{{a^2}}}\]

Посчитаем ответ:

\[E = \frac{{2 \cdot 9 \cdot {{10}^9} \cdot 0,1 \cdot {{10}^{ – 6}}}}{{{1^2}}} = 1800\;В/м\]