Условие задачи:
Шарик массой 10 г с зарядом 100 мкКл подвешен на тонкой нити длиной 50 см в однородном электрическом поле напряженностью 100 В/м, силовые линии которого горизонтальны и направлены справа налево. Шарик отвели влево так, что он оказался на 40 см ниже точки подвеса нити, и отпустили. Найдите силу натяжения нити в момент прохождения шариком нижней точки траектории.
Задача №6.3.58 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=10\) г, \(q=100\) мкКл, \(l=50\) см, \(E=100\) В/м, \(\Delta h=40\) см, \(T-?\)
Решение задачи:
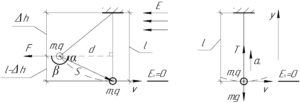Будем решать эту задачу с конца. Для того, что найти силу натяжения нити \(T\) в момент прохождения шариком нижней точки траектории, нужно записать для шарика в этом положении второй закон Ньютона в проекции на ось \(y\) (смотрите схему справа):
\[T – mg = m{a_ц}\;\;\;\;(1)\]
Центростремительное ускорение \(a_ц\) легко найти по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{l}\;\;\;\;(2)\]
Здесь \(\upsilon\) – скорость шарика в нижней точке траектории, \(l\) – длина нити, которая в данном случае равна радиусу кривизны траектории движения шарика. Подставим (2) в (1), тогда получим следующее:
\[T – mg = \frac{{m{\upsilon ^2}}}{l}\]
\[T = mg + \frac{{m{\upsilon ^2}}}{l}\;\;\;\;(3)\]
Теперь, чтобы найти скорость \(\upsilon\), необходимо применить закон сохранения энергии. Работа электрического поля \(A\) равна изменению полной механической энергии шарика. Если выбрать нуль потенциальной энергии на уровне нижней точки траектории шарика, то в конце он будет обладать только кинетической энергией, а в начале – потенциальной (несложно понять, что здесь шарик находится на высоте \(\left(l – \Delta h\right)\) от нижней точки – смотрите схему слева). Справедливо записать:
\[A = \frac{{m{\upsilon ^2}}}{2} – mg\left( {l – \Delta h} \right)\;\;\;\;(4)\]
Давайте теперь разберёмся с работой электрического поля \(A\). Вообще, любая работа равна скалярному произведению вектора силы на вектор перемещения, и если вспомнить математику, то это скалярное произведение можно записать как произведение модулей (т.е. абсолютных величин) указанных векторов на косинус угла между ними. То есть:
\[A = \overrightarrow F \cdot \overrightarrow S = F \cdot S \cdot \cos \beta = – F \cdot S \cdot \cos \alpha \]
Здесь мы учли тот факт, что \(\alpha + \beta = 90^\circ\) и поэтому \(\cos \beta = – \cos \alpha\).
Произведение \(S \cdot \cos \alpha\) равно \(d\) – это прекрасно видно на схеме, поэтому:
\[A = – F \cdot d\;\;\;\;(5)\]
Длину отрезка \(d\) можно найти из теоремы Пифагора:
\[d = \sqrt {{l^2} – \Delta {h^2}} \;\;\;\;(6)\]
Величину электрической силы \(F\) найдём как произведение напряжённости поля \(E\) на заряд шарика \(q\):
\[F = Eq\;\;\;\;(7)\]
Подставим (6) и (7) в (5), тогда:
\[A = – Eq\sqrt {{l^2} – \Delta {h^2}} \]
Полученное подставим в (4) и выразим \(\frac{{m{\upsilon ^2}}}{2}\) – для чего, Вы узнаете позже:
\[ – Eq\sqrt {{l^2} – \Delta {h^2}} = \frac{{m{\upsilon ^2}}}{2} – mg\left( {l – \Delta h} \right)\]
\[\frac{{m{\upsilon ^2}}}{2} = mg\left( {l – \Delta h} \right) – Eq\sqrt {{l^2} – \Delta {h^2}} \;\;\;\;(8)\]
Выполним следующий трюк – запишем формулу (3) в следующем виде:
\[T = mg + \frac{{2m{\upsilon ^2}}}{{2l}}\]
\[T = mg + \frac{2}{l} \cdot \frac{{m{\upsilon ^2}}}{2}\]
В эту формулу подставим выражение (8), имеем:
\[T = mg + \frac{2}{l} \cdot \left( {mg\left( {l – \Delta h} \right) – Eq\sqrt {{l^2} – \Delta {h^2}} } \right)\]
Проведём некоторые преобразования, чтобы получить окончательную формулу:
\[T = \frac{{mgl}}{l} + \frac{{mg\left( {2l – 2\Delta h} \right)}}{l} – \frac{{2Eq\sqrt {{l^2} – \Delta {h^2}} }}{l}\]
\[T = \frac{{mg\left( {3l – 2\Delta h} \right)}}{l} – \frac{{2Eq\sqrt {{l^2} – \Delta {h^2}} }}{l}\]
Произведём расчёт численного ответа:
\[T = \frac{{0,01 \cdot 10 \cdot \left( {3 \cdot 0,5 – 2 \cdot 0,4} \right)}}{{0,5}} + \frac{{2 \cdot 100 \cdot 100 \cdot {{10}^{ – 6}} \cdot \sqrt {{{0,5}^2} – {{0,4}^2}} }}{{0,5}} = 0,128\;Н\]
Ответ: 0,128 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
6.3.57 Заряды q1=2 мкКл и q2=5 мкКл расположены на расстоянии AB=40 см друг от друга
6.3.59 Внутри шарового металлического слоя, внутренний и внешний радиусы которого
6.3.60 По тонкому проволочному кольцу радиуса 3 см равномерно распределен заряд 10^(-9) Кл
Здравствуйте, почему напряженность на уровне неотведенного влево шарика равна 0?
Это не напряженность, а нулевой уровень потенциальной энергии.
Потенциальная энергия в верхней точке, равняется кинетической в нижней точке, тогда mυ^2\2=mg(l—Δh)(4). И как электрическое поле может повлиять на натяжение нити, если оно находится на оси x, а натяжение нити на оси y ?
Возможно поле влияет на линейную скорость, что в свою очередь влияет на центростремительное ускорение ? Тогда, mg(l—Δh)=mU^2\2 и потому A+mg(l—Δh)=mV^2\2.
Я правильно рассуждаю ?
Верно, смотрите формулу (4), из нее становится все понятно.
Однако ответы у нас получились разные:
Мой ответ Т=580 мН
Решение в общем виде совпадает с моим?
1. Почему при переходе шарика из крайнего левого положения в положение равновесия учтена работа только силы электрического поля? Шарик ещё движется и в гравитационном поле Земли. Работа силы тяжести отнюдь не равна нулю.
2 Здесь закон сохранения энергии удобно записать в форме теоремы о кинетической энергии, поскольку кулоновская сила и сила тяжести являются внешними силами.
3. Наконец, работа каждой из этих сил не зависит от формы траектории, то вместо криволинейной траектории можно рассматривать перемещение вдоль траектории, образующей треугольник ( на рис. он не назван)
1. Учтена, смотрите внимательно на формулу (4).
2. Дело вкуса и привычки. Я всегда повторяю, что мои решения – не истина в последней инстанции. Ваш вариант, наверное, для учащихся будет более понятным, хотя математически там будут практически одинаковые равенства.
3. Траектория в решении меня не интересует, мне нужен лишь вектор перемещения.
Здравствуйте. Это сайт мне понравился тем, что схемы к задачам нарисованы не от руки, а в профессиональном графическом редакторе, поэтому видно всю страницу сразу в отличие от других решебников, где пишут, рисуют схемы от руки и хрен поймёшь в этих каракулях, что, о чём написано. Но здесь хотелось, чтоб новые задачи появлялись чаще (хотя бы раз в неделю, максимум раз в 3 недели). Последняя новая задача появилась у вас 13.12.2017 (почти 2 месяца прошло и ничего нового).
Новые задачи обязательно будут!
Здравствуйте , касаемо задачи 6.3.58 , на мой взгляд , вырыжение 6. , для d выведено неправильно . Должно быть под корнем l в квадрате минус( ( l-дельта h ) в квадрате). С уважением Егор .
Все правильно ….