Решение: Определить электроемкость батареи конденсаторов, изображенной на рисунке

Условие задачи:

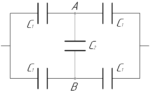Определить электроемкость батареи конденсаторов, изображенной на рисунке, если \(C_1=2\) мкФ, \(C_2=4\) мкФ.

Задача №6.4.43 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(C_1=2\) мкФ, \(C_2=4\) мкФ, \(C-?\)

Решение задачи:

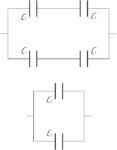Обратите Ваше внимание на то, что схема симметричная, а это значит, что потенциалы точек A и B будет одинаковыми. Это означает, что конденсатор с электроемкостью \(C_2\) будет незаряжен (так как разности потенциалов между его обкладками нет), поэтому этот конденсатор можно легко исключить, и исходная схема примет следующий вид (смотрите рисунок справа).

Полученную схему легко преобразовать в другую. Так как два конденсатора в верхней и нижней ветви соединены последовательно, то заменим их эквивалентной электроемкостью \(C_3\), которую можно найти таким образом:

\[\frac{1}{{{C_3}}} = \frac{1}{{{C_1}}} + \frac{1}{{{C_1}}}\]

\[\frac{1}{{{C_3}}} = \frac{2}{{{C_1}}}\]

\[{C_3} = \frac{{{C_1}}}{2}\;\;\;\;(1)\]

А так как конденсаторы \(C_3\) соединены последовательно, то искомая электроемкость \(C\) равна:

\[C = {C_3} + {C_3}\]

Учитывая (1), получим:

\[C = \frac{{{C_1}}}{2} + \frac{{{C_1}}}{2}\]

\[C = {C_1}\]

\[C = 2\;мкФ\]