Условие задачи:

Два одинаковых шарика подвешены на нитях в воздухе так, что их поверхности соприкасаются. После того как каждому шарику сообщили заряд 0,4 мкКл, они разошлись на угол 60°. Найти массу шариков, если расстояние от центров шариков до точки подвеса 0,2 м.

Задача №6.1.25 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q=0,4\) мкКл, \(\alpha=60^\circ\), \(l=0,2\) м, \(m-?\)

Решение задачи:

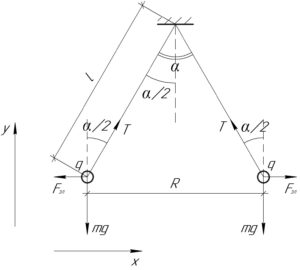Покажем на схеме тот момент, когда шарики будут находиться в равновесии. На каждый шарик действуют три силы: сила тяжести \(mg\), кулоновская сила отталкивания \(F_{эл}\) и сила натяжения нити \(T\) (смотрите схему). Запишем первый закон Ньютона для левого шарика (вообще можно рассматривать любой) в проекции на обе оси координат:

\[\left\{ \begin{gathered}
{T_0}\cos \frac{\alpha }{2} = mg \hfill \\
{T_0}\sin \frac{\alpha }{2} = {F_{эл}} \hfill \\
\end{gathered} \right.\]

Поделим нижнее уравнение на верхнее, тогда:

\[tg\frac{\alpha }{2} = \frac{{{F_{эл}}}}{{mg}}\;\;\;\;(1)\]

Закон Кулона гласит, что сила взаимодействия (отталкивания, в данном случае) \(F_{эл}\) зарядов прямо пропорциональна величине этих зарядов \(q\) и обратно пропорциональна расстоянию \(R\) между ними, поэтому:

\[{F_{эл}} = \frac{{k{q^2}}}{{{R^2}}}\]

Коэффициент пропорциональности \(k\) равен 9·10⁹ Н·м²/Кл².

Из схемы к решению видно, что:

\[R = 2l\sin \frac{\alpha }{2}\]

Поэтому:

\[{F_{эл}} = \frac{{k{q^2}}}{{4{l^2}{{\sin }^2}\frac{\alpha }{2}}}\]

Полученное выражение подставим в формулу (1):

\[tg\frac{\alpha }{2} = \frac{{k{q^2}}}{{4mg{l^2}{{\sin }^2}\frac{\alpha }{2}}}\]

\[m = \frac{{k{q^2}}}{{4g{l^2}{{\sin }^2}\frac{\alpha }{2}tg\frac{\alpha }{2}}}\]

Задача решена в общем виде. Посчитаем численный ответ к задаче:

\[m = \frac{{9 \cdot {{10}^9} \cdot {{\left( {0,4 \cdot {{10}^{ — 6}}} \right)}^2}}}{{4 \cdot 10 \cdot {{0,2}^2} \cdot {{\sin }^2}\frac{{60^\circ }}{2} \cdot tg\frac{{60^\circ }}{2}}} = 0,0062\;кг = 6,2\;г\]

Ответ: 6,2 г.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

6.1.24 В вертикальной трубке, заполненной воздухом, закреплен точечный заряд 5 мкКл
6.1.26 Два шарика массой по 1 г подвешены на нитях длиной 0,5 м в одной точке. После
6.1.27 Два маленьких проводящих шарика подвешены на длинных непроводящих нитях