Решение: Четыре одинаковых заряда 40 мкКл расположены в вершинах квадрата со стороной

Условие задачи:

Четыре одинаковых заряда 40 мкКл расположены в вершинах квадрата со стороной \(a=2\) м. Какова будет напряженность поля на расстоянии \(2a\) от центра квадрата на продолжении диагонали?

Задача №6.2.29 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(q=40\) мкКл, \(a=2\) м, \(L=2a\), \(E-?\)

Решение задачи:

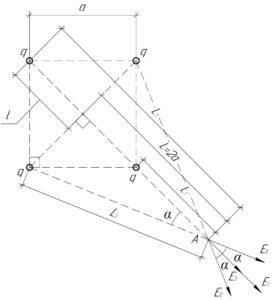Начнём решать задачу издалека, пусть \(l\) – это половина длины диагонали квадрата. Длину диагонали квадрата можно найти по теореме Пифагора, поэтому:

\[l = \frac{{\sqrt {{a^2} + {a^2}} }}{2} = \frac{{\sqrt 2 a}}{2}\;\;\;\;(1)\]

Назовём точку на расстоянии \(2a\) от центра квадрата на продолжении диагонали – точкой A.

Самый ближний заряд \(q\) находится от точки A на расстоянии \(L_1\), которое, очевидно, можно определить из выражения:

\[{L_1} = L – l\]

Учитывая (1) и то, что по условию \(L=2a\), получим:

\[{L_1} = 2a – \frac{{\sqrt 2 a}}{2}\]

\[{L_1} = \frac{{a\left( {4 – \sqrt 2 } \right)}}{2}\;\;\;\;(2)\]

Два заряда \(q\), лежащие по обе стороны от указанной в условии диагонали, находятся от точки A на расстоянии \(L_2\), которое можно найти по теореме Пифагора:

\[L_2^2 = {L^2} + {l^2}\]

Аналогично, учитывая (1) и то, что по условию \(L=2a\), получим:

\[L_2^2 = 4{a^2} + \frac{{{a^2}}}{2}\]

\[L_2^2 = \frac{{9{a^2}}}{2}\;\;\;\;(3)\]

В данном случае квадратный корень можно и не извлекать.

Самый дальний заряд \(q\) находится от точки A на расстоянии \(L_3\), которое легко найдём по такой очевидной формуле:

\[{L_3} = L + l\]

\[{L_3} = 2a + \frac{{\sqrt 2 a}}{2}\]

\[{L_3} = \frac{{a\left( {4 + \sqrt 2 } \right)}}{2}\;\;\;\;(4)\]

Отлично, мы определились со всеми расстояниями, теперь перейдём к напряженностям. Очевидно, что напряженности полей, создаваемых самым ближним и дальним зарядами \(q\), будут направлены по диагонали, причём модули напряженностей (принимая во внимания равенства (2) и (4)) можно будет найти по таким формулам:

\[\left\{ \begin{gathered}
{E_1} = \frac{{4kq}}{{{a^2}{{\left( {4 – \sqrt 2 } \right)}^2}}} \hfill \\
{E_3} = \frac{{4kq}}{{{a^2}{{\left( {4 + \sqrt 2 } \right)}^2}}} \hfill \\
\end{gathered} \right.\]

Каждый из двух зарядов \(q\), лежащих по обе стороны от диагонали, будут создавать в точке A электрическое поле напряженностью \(E_0\), модуль которой равен (учитывая равенство (3)):

\[{E_0} = \frac{{kq}}{{L_2^2}} = \frac{{2kq}}{{9{a^2}}}\]

Поскольку эти два заряда имеют равный заряд и находятся на одинаковом расстоянии от точки A, то они будут создавать в этой точке суммарное электростатическое поле, напряженность которого \(E_2\) также направлена по диагонали. Модуль напряженности \(E_2\) можно найти по такой формуле (по сути – это сумма проекций напряженностей от этих зарядов на продолжение диагонали):

\[{E_2} = 2{E_0}\cos \alpha \]

Косинус угла \(\alpha\) легко найти, используя схему к решению и теорему Пифагора:

\[\cos \alpha = \frac{L}{{\sqrt {{L^2} + {l^2}} }} = \frac{{2a}}{{\sqrt {4{a^2} + \frac{{{a^2}}}{2}} }} = \frac{{2a\sqrt 2 }}{{3a}} = \frac{{2\sqrt 2 }}{3}\]

Поэтому:

\[{E_2} = 2 \cdot \frac{{2kq}}{{9{a^2}}} \cdot \frac{{2\sqrt 2 }}{3}\]

\[{E_2} = \frac{{8\sqrt 2 kq}}{{27{a^2}}}\]

В итоге, поскольку все напряженности \(E_1\), \(E_2\) и \(E_3\) лежат на одной прямой и сонаправлены, то:

\[E = {E_1} + {E_2} + {E_3}\]

\[E = \frac{{4kq}}{{{a^2}{{\left( {4 – \sqrt 2 } \right)}^2}}} + \frac{{4kq}}{{{a^2}{{\left( {4 + \sqrt 2 } \right)}^2}}} + \frac{{8\sqrt 2 kq}}{{27{a^2}}}\]

\[E = \frac{{4kq}}{{{a^2}}}\left( {\frac{1}{{{{\left( {4 – \sqrt 2 } \right)}^2}}} + \frac{1}{{{{\left( {4 + \sqrt 2 } \right)}^2}}} + \frac{{2\sqrt 2 }}{{27}}} \right)\]

Произведём некоторые математические преобразования:

\[E = \frac{{4kq}}{{{a^2}}}\left( {\frac{{{{\left( {4 + \sqrt 2 } \right)}^2} + {{\left( {4 – \sqrt 2 } \right)}^2}}}{{{{\left( {4 – \sqrt 2 } \right)}^2}{{\left( {4 + \sqrt 2 } \right)}^2}}} + \frac{{2\sqrt 2 }}{{27}}} \right)\]

\[E = \frac{{4kq}}{{{a^2}}}\left( {\frac{{18 + 8\sqrt 2 + 18 – 8\sqrt 2 }}{{196}} + \frac{{2\sqrt 2 }}{{27}}} \right)\]

\[E = \frac{{4kq}}{{{a^2}}}\left( {\frac{9}{{49}} + \frac{{2\sqrt 2 }}{{27}}} \right)\]

Задача решена в общем виде, теперь посчитаем численный ответ к задаче:

\[E = \frac{{4 \cdot 9 \cdot {{10}^9} \cdot 40 \cdot {{10}^{ – 6}}}}{{{2^2}}}\left( {\frac{9}{{49}} + \frac{{2\sqrt 2 }}{{27}}} \right) = 103834,8\;В/м \approx 104\;кВ/м\]