Условие задачи:

Цилиндр радиуса $R$, расположенный вертикально, вращается вокруг своей оси с постоянной угловой скоростью $\omega$. На внутренней поверхности цилиндра находится небольшое тело, вращающееся вместе с цилиндром. При какой минимальной величине коэффициента трения скольжения между телом и поверхностью цилиндра, тело не будет скользить вниз?

Задача №2.4.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$R$, $\omega$, $\mu-?$

Решение задачи:

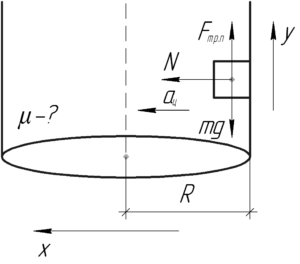Покажем на схеме все силы, действующие на тело. Второй закон Ньютона, записанный в проекции на ось $x$, даст такое равенство:

$$N = m{a_ц}$$

Так как в условии задачи дана угловая скорость вращения цилиндра $\omega$, то выразим центростремительное ускорение через неё:

$${a_ц} = {\omega ^2}R$$

$$N = m{\omega ^2}R\;\;\;\;(1)$$

Вдоль оси $y$ действуют две силы: сила тяжести $mg$ и сила трения покоя $F_{тр.п}$. Первый закон Ньютона в проекции на эту ось выглядит так:

$${F_{тр.п}} = mg\;\;\;\;(2)$$

Чтобы найти минимальный коэффициент трения $\mu$, сила трения покоя должна принимать максимальное значение. Это максимальное значение силы трения покоя можно найти по формуле:

$${F_{тр.п}} = \mu N$$

Учитывая (1), эта формула примет вид:

$${F_{тр.п}} = \mu m{\omega ^2}R$$

Приравняем с (2), тогда получи следующее:

$$mg = \mu m{\omega ^2}R$$

$$\mu  = \frac{g}{{{\omega ^2}R}}$$

Задача решена.

Ответ: $\mu  = \frac{g}{{{\omega ^2}R}}$.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.41 Цилиндр радиуса R, расположенный вертикально, вращается вокруг своей оси
2.4.43 В сельском хозяйстве применяются дисковые разбрасыватели удобрений. Какой должна
2.5.1 Во сколько раз уменьшится сила тяготения тела к Земле при удалении его