Условие задачи:

Трактор массой 8 т проходит по мосту со скоростью 36 км/ч. Какова сила давления трактора на середину моста, если мост выпуклый и имеет радиус кривизны 200 м?

Задача №2.4.11 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

$m=8$ т, $\upsilon=36$ км/ч, $R=200$ м, $P-?$

Решение задачи:

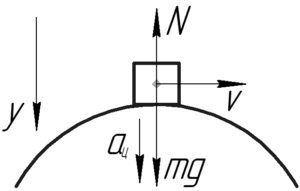Покажем на рисунке схематично трактор, находящийся по середине выпуклого моста. Запишем второй закон Ньютона в проекции на ось $y$:

$$mg — N = m{a_ц}$$

Зная скорость трактора $\upsilon$ в этой точке и радиус кривизны моста $R$, легко найдем центростремительное ускорение:

$${a_ц} = \frac{{{\upsilon ^2}}}{R}$$

Тогда первое равенство примет такой вид:

$$mg — N = m\frac{{{\upsilon ^2}}}{R}$$

Вообще, искомая сила давления трактора на мост $P$ равна силе реакции опоры $N$ по третьему закону Ньютона:

$$P = N$$

Поэтому:

$$mg — P = m\frac{{{\upsilon ^2}}}{R}$$

В итоге сила давления трактора на мост равна:

$$P = m\left( {g — \frac{{{\upsilon ^2}}}{R}} \right)$$

Переведем массу трактора и его скорость в единицы системы СИ:

$$8\; т = 8000\; кг$$

$$36\; км/ч = \frac{{36 \cdot 1000}}{{1 \cdot 3600}}\; м/с = 10\; м/с$$

Остается только посчитать ответ:

$$P = 8000 \cdot \left( {10 — \frac{{{{10}^2}}}{{200}}} \right) = 76000\; Н = 76\; кН$$

Ответ: 76 кН.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.4.10 Поезд движется по закруглению радиуса 765 м со скоростью 72 км/ч. Определить
2.4.12 Конькобежец движется по закруглению ледяной дорожки радиусом 2,5 м со скоростью
2.4.13 Шоссе имеет вираж с уклоном 10 градусов при радиусе закругления дороги в 100 м