Условие задачи:
Тело массой 2 кг тянут по гладкой горизонтальной поверхности с помощью пружины, которая при движении растянулась на 2 см. Жесткость пружины 200 Н/м. Определить ускорение, с которым движется тело.
Задача №2.6.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=2\) кг, \(x=2\) см, \(k=200\) Н/м, \(a-?\)
Решение задачи:
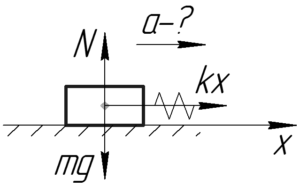Понятно, что в данном случае сила упругости будет сообщать телу некоторое ускорение. Сила упругости по закону Гука численно равна \(kx\). Запишем второй закон Ньютона в проекции на ось \(x\):
\[kx = ma\]
Тогда искомое ускорение тела \(a\) найдем по формуле:
\[a = \frac{{kx}}{m}\]
Переведем удлинение пружины в систему СИ и посчитаем ответ:
\[2\; см = \frac{2}{{100}}\; м = 0,02\; м\]
\[a = \frac{{200 \cdot 0,02}}{2} = 2\; м/с^2\]
Ответ: 2 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.6.8 Найти удлинение буксирного троса с жесткостью 100 кН/м при буксировке автомобиля
2.6.10 Тело массой 2 кг тянут по горизонтальной поверхности с помощью пружины, которая
2.6.11 Сила в 6 Н растягивает пружину на 2 см. Какую работу надо произвести, чтобы
Объясните, пожалуйста, почему сила упругости направлена вправо? Разве сила упругости не должна быть направлена в сторону, противоположную деформации пружины? И почему мы не учитываем силу, с которой тянут данное тело?
Ящик массой 20 кг тянут по ровнму полу с горизонтальной (параллельной полу) силой = 30 Н. Коэффициент трения между ящиком и полом составляет f = 0,1. Найдите ускорение, с которым движется ящик. Какой должна быть масса ящика, если он движется с той же силой, по той же поверхности с постоянной скоростью?
30 – 0.1*20 = 28N
a = 28/20 = 1.4
подскажите пожалуйста, правильно ли я нашла ускорение?
и как массу найти при постоянной скорости?
Вы забыли умножить на ускорение свободного падения при нахождении силы трения.
Запишем второй закон Ньютона в проекции на ось \(x\):\[F – fmg = ma\]Откуда найдем ускорение \(a\):\[a = \frac{{F – fmg}}{m}\]\[a = \frac{{30 – 0,1 \cdot 20 \cdot 10}}{{20}} = 0,5\;м/с^2\]Для случая движения с постоянной скоростью запишем первый закон Ньютона в проекции на ту же ось:\[F – fmg = 0\]Откуда масса равна:\[m = \frac{F}{{fg}}\]\[m = \frac{{30}}{{0,1 \cdot 10}} = 30\;кг\]
классно
