Условие задачи:
Тело массой 2 кг начинает движение под действием постоянной по направлению силы. Модуль силы со временем увеличивается линейно, возрастая от 0 до 4 Н за 2 с. Какова скорость тела в конце второй секунды?
Задача №2.1.67 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=2\) кг, \(F_0=0\) Н, \(F_1=4\) Н, \(\tau=2\) с, \(\upsilon \left( \tau \right) — ?\)
Решение задачи:
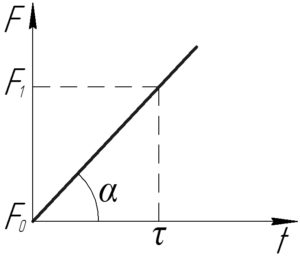Нарисуем график изменения силы от времени. Так как график функции линейный и проходит через начало координат, то функцию изменения силы можно представить в виде:
\[F\left( t \right) = kt\]
Коэффициент \(k\) легко определить с помощью графика, так как он равен тангенсу угла наклона прямой.
\[k = tg\alpha = \frac{{{F_1} — {F_0}}}{\tau }\]
\[F\left( t \right) = \frac{{{F_1} — {F_0}}}{\tau }t\]
Согласно второму закону Ньютона ускорение тела \(a\left( t \right)\) прямо пропорционально приложенной к нему силе \( F\left( t \right)\) и обратно пропорциональна массе тела \(m\).
\[a\left( t \right) = \frac{{F\left( t \right)}}{m}\]
\[a\left( t \right) = \frac{{{F_1} — {F_0}}}{{m\tau }}t\]
Функцию ускорения тела можно найти как первую производную от функции скорости тела.
\[a\left( t \right) = \upsilon’ \left( t \right)\]
Значит чтобы найти функцию изменения скорости, нужно взять неопределенный интеграл от функции изменения ускорения.
\[\upsilon \left( t \right) = \int {a\left( t \right)dt} \]
\[\upsilon \left( t \right) = \int {\frac{{{F_1} — {F_0}}}{{m\tau }}tdt} = \frac{{{F_1} — {F_0}}}{{m\tau }}\int {tdt} = \frac{{\left( {{F_1} — {F_0}} \right){t^2}}}{{2m\tau }} + C\]
Теперь определим постоянную интегрирования \(C\). Так как сказано, что «тело начинало своё движение», то:
\[\upsilon \left( 0 \right) = 0\]
\[\upsilon \left( 0 \right) = \frac{{\left( {{F_1} — {F_0}} \right){0^2}}}{{2m\tau }} + C = 0 \Rightarrow C = 0\]
\[\upsilon \left( t \right) = \frac{{\left( {{F_1} — {F_0}} \right){t^2}}}{{2m\tau }}\]
В итоге, скорость в конце второй секунды равна:
\[\upsilon \left( \tau \right) = \frac{{\left( {{F_1} — {F_0}} \right){\tau ^2}}}{{2m\tau }}\]
\[\upsilon \left( \tau \right) = \frac{{\left( {4 — 0} \right){2^2}}}{{2 \cdot 2 \cdot 2}} = 2\; м/с = 7,2\; км/ч\]
Ответ: 7,2 км/ч.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.66 Стержень длиной 0,9 м движется с ускорением под действием приложенной к его
2.1.68 Что покажут пружинные весы в лифте при измерении веса груза массой 1 кг
2.1.69 Хоккейная шайба, имея начальную скорость 5 м/с, скользит до удара о борт площадки