Условие задачи:
Струя сечением 6 см2 ударяет из брандспойта в стенку под углом 60° к нормали и под тем же углом упруго “отражается” от нее. Скорость течения воды в струе 15 м/с. С какой силой она давит на стену?
Задача №2.1.74 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S=6\) см2, \(\alpha=60^\circ\), \(\upsilon=15\) м/с, \(F-?\)
Решение задачи:
Во-первых, согласно третьему закона Ньютона, с какой силой взаимодействует струя со стенкой, с такой же силой действует стенка на струю.
По второму закону Ньютона, записанному в общем виде, сила, действующая со стороны стенки на струю, есть отношение изменения импульса струи к времени взаимодействия.
\[F = \frac{{\Delta p}}{{\Delta t}}\]
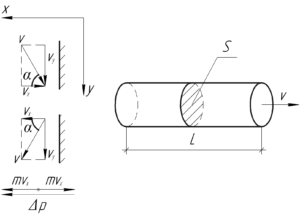
При упругом ударе (отражении) угол между вектором скорости и нормалью к стенке не меняется. Рассмотрим проекции скорости струи в проекции на оси координат до и после удара (отражения).
Видно, что проекция скорости на ось \(y\) не меняется, значит не меняется и проекция импульса на эту ось, поэтому вдоль этой оси не действует сила со стороны стенки.
Проекция скорости на ось \(x\) меняется по направлению, значит изменение импульса составит:
\[\Delta p = 2m{\upsilon _x} = 2m\upsilon \cdot \cos \alpha \]
В итоге сила давления струи на стенку равна:
\[F = \frac{{2m\upsilon \cdot \cos \alpha }}{{\Delta t}}\]
Так как струя является объектом протяженной массы цилиндрической формы, то верно следующее:
\[m = \rho V = \rho SL\]
Здесь \(\rho\) – плотность воды, равная 1000 кг/м3.
\[F = \frac{{2\rho SL\upsilon \cdot \cos \alpha }}{{\Delta t}}\]
Отношение \(\frac{L}{\Delta t}\) при стремлении времени к нулю равно скорости струи \(\upsilon\).
\[\upsilon = \frac{L}{{\Delta t}} \Rightarrow F = 2\rho S{\upsilon ^2} \cdot \cos \alpha \]
Переведем площадь струи в единицы системы СИ.
\[6\; см^2 = \frac{6}{{{{10}^4}}}\; м^2 = 6 \cdot {10^{ – 4}}\; м^2\]
Численный ответ равен:
\[F = 2 \cdot {10^3} \cdot 6 \cdot {10^{ – 4}} \cdot {15^2} \cdot \cos 60^\circ = 135\; Н\]
Ответ: 135 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.73 На гладкой поверхности лежит доска массой 5 кг, на ней находится тело массой 3 кг
2.1.75 На скользкой дороге коэффициент трения между дорогой и колесами мотоцикла
2.1.76 Груз массой 10 кг привязан к свободно свисающему концу веревки, намотанной
А почему при очень малом t мы получаем что L = v. Там же если при очень малом времени число будет стремиться к бесконечности и не будет иметь связи с v, вроде как?
Если в задаче сказано под каким-то углом к нормали, это значит этот угол к горизонту, правильно?
Нормаль – это перпендикуляр к плоскости, если говорить просто. В данном случае стенка вертикальная, значит нормаль направлена горизонтально, поэтому в данной задаче угол к нормали и угол к горизонту – это одно и то же. Но в общем случае следует пользоваться определением из первого предложения данного комментария.
Пусть за время \({\Delta t}\) струя прошла расстояние \({\Delta L}\). Тогда отношение \(\frac{{\Delta L}}{{\Delta t}}\) есть средняя скорость движения струи.
Если же это отношение рассматривать в пределе при \(\Delta t \to 0\), то вместо средней скорости мы уже получаем мгновенную скорость струи.
Вы упустили тот факт, что при \(\Delta t \to 0\) расстояние \({\Delta L}\) тоже стремиться к малой величине
Я не понял, почему при отражении импульс удваивается?
Потому что изменение импульса (как и сам импульс) – величина векторная, которую можно найти следующим образом:\[\Delta \overrightarrow p = \overrightarrow p – \overrightarrow {{p_0}} \]На рисунке видно, что \(\overrightarrow {{p_0}} = m\overrightarrow {{\upsilon _x}} \), а \(\overrightarrow p = – m\overrightarrow {{\upsilon _x}} \)Тогда:\[\Delta \overrightarrow p = – m\overrightarrow {{\upsilon _x}} – m\overrightarrow {{\upsilon _x}} \]\[\Delta \overrightarrow p = – 2m\overrightarrow {{\upsilon _x}} \]
Спасибо
у вас в подсчетах косинус 0.5 а должен быть корень из 3 делить на 2
Нет, так как \(\cos 60^\circ = \frac{1}{2}\).
Почему косинус ,а не синус ?
Потому что \(\upsilon_x\) является прилежащим к углу \(\alpha\) катетом в векторном треугольнике (смотрите рисунок)
А почему L на t делить надо объясните пожалуйста:)
Пусть струя проходит за время t расстояние L, тогда её скорость можно найти, разделив L на t