Решение: Шарик на нити отклонили от вертикали на 60 градусов и отпустили без начальной

Условие задачи:

Шарик на нити отклонили от вертикали на 60° и отпустили без начальной скорости. В момент, когда шарик достиг вертикального положения, он ударился о вертикальную стенку и потерял половину своей энергии. На какой угол он отклонится после удара?

Задача №2.8.53 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=60^\circ\), \(\gamma=\frac{1}{2}\), \(\beta-?\)

Решение задачи:

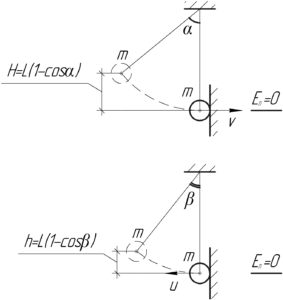Запишем трижды закон сохранения энергии:

для начального момента, когда шарик отклонен на угол \(\alpha\), и в момент непосредственно перед ударом;
до и после неупругого удара о стенку, при этом не забывая о потерях энергии;
сразу после удара шарика о стенку и в момент, когда шарик отклонится уже на угол \(\beta\).

\[\left\{ \begin{gathered}
mgL\left( {1 — \cos \alpha } \right) = \frac{{m{\upsilon ^2}}}{2} \;\;\;\;(1)\hfill \\
\frac{{m{\upsilon ^2}}}{2} = \frac{{m{u^2}}}{2} + Q \;\;\;\;(2)\hfill \\
\frac{{m{u^2}}}{2} = mgL\left( {1 — \cos \beta } \right) \;\;\;\;(3)\hfill \\
\end{gathered} \right.\]

Поделим равенство (3) на равенство (1):

\[\frac{{1 — \cos \beta }}{{1 — \cos \alpha }} = {\left( {\frac{u}{\upsilon }} \right)^2}\;\;\;\;(4)\]

Обе части равенства (2) поделим на \(\frac{{m{\upsilon ^2}}}{2}\), тогда:

\[1 = {\left( {\frac{u}{\upsilon }} \right)^2} + \frac{{2Q}}{{m{\upsilon ^2}}}\]

Так как из условия понятно, что \(\gamma = \frac{{2Q}}{{m{\upsilon ^2}}}\), то:

\[1 = {\left( {\frac{u}{\upsilon }} \right)^2} + \gamma \]

\[{\left( {\frac{u}{\upsilon }} \right)^2} = 1 — \gamma \;\;\;\;(5)\]

Посмотрев на формулы (4) и (5), справедливо записать следующее:

\[\frac{{1 — \cos \beta }}{{1 — \cos \alpha }} = 1 — \gamma \]

Остаётся только выполнить алгебраические преобразования.

\[1 — \cos \beta = \left( {1 — \gamma } \right)\left( {1 — \cos \alpha } \right)\]

\[1 — \cos \beta = 1 — \cos \alpha — \gamma + \gamma \cos \alpha \]