Условие задачи:
Шарик массой 200 г на нити длиной 3 м описывает в горизонтальной плоскости окружность радиусом 1 м. Каков период его обращения?
Задача №2.4.27 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=200\) г, \(l=3\) м, \(R=1\) м, \(T-?\)
Решение задачи:
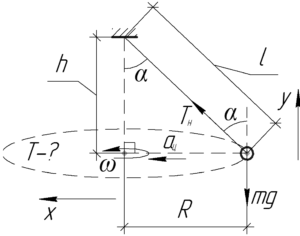 На шарик действуют всего две силы: сила тяжести \(mg\) и сила натяжения нити \(T_н\). Запишем первый закон Ньютона в проекции на ось \(y\) и второй закон Ньютона в проекции на ось \(x\):
На шарик действуют всего две силы: сила тяжести \(mg\) и сила натяжения нити \(T_н\). Запишем первый закон Ньютона в проекции на ось \(y\) и второй закон Ньютона в проекции на ось \(x\):
\[\left\{ \begin{gathered}
{T_н} \cdot \cos \alpha = mg \hfill \\
{T_н} \cdot \sin \alpha = m{a_ц} \hfill \\
\end{gathered} \right.\]
Вспомним из кинематики вращательного движения следующие формулы:
\[{a_ц} = {\omega ^2}R\]
\[\omega = \frac{{2\pi }}{T}\]
Тогда формула связи центростремительного ускорение и периода выглядит так:
\[{a_ц} = \frac{{4{\pi ^2}}}{{{T^2}}}R\]
Наша система примет вид:
\[\left\{ \begin{gathered}
{T_н} \cdot \cos \alpha = mg \hfill \\
{T_н} \cdot \sin \alpha = \frac{{4{\pi ^2}}}{{{T^2}}}mR \hfill \\
\end{gathered} \right.\]
Поделим нижнее равенство на верхнее, тогда имеем:
\[tg\alpha = \frac{{4{\pi ^2}R}}{{g{T^2}}}\]
\[T = 2\pi \sqrt {\frac{R}{{g \cdot tg\alpha }}} \]
На схеме видно, что:
\[tg\alpha = \frac{R}{h}\]
По теореме Пифагора:
\[h = \sqrt {{l^2} — {R^2}} \]
\[tg\alpha = \frac{R}{{\sqrt {{l^2} — {R^2}} }}\]
В конце концов, итоговая формула будет выглядеть так:
\[T = 2\pi \sqrt {\frac{{\sqrt {{l^2} — {R^2}} }}{g}} \]
Посчитаем ответ:
\[T = 2 \cdot 3,14\sqrt {\frac{{\sqrt {{3^2} — {1^2}} }}{{10}}} = 3,34\; с\]
Интересно, что период вращения шарика не зависит от его массы.
Ответ: 3,34 с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.26 Подвешенный на нити шарик массой 0,3 кг совершает колебания в вертикальной
2.4.28 Тело массой 4 кг вращают в вертикальной плоскости с помощью резинового шнура
2.4.29 К потолку лифта на нити длиной 40 см прикреплен шар массой 800 г, который вращается
Можете пожалуйста рисунок сделать чётче, а то непонятно немного, заранее спасибо
Рисунок чётче некуда, можно ещё щёлкнуть по рисунку, получится увеличенный, чётче будет видно.
Подскажите пожалуйста, как и в каком направлении спроектировать силу натяжения на ось ОХ? (дело в знаках)
Проекция силы натяжения \(T_{н}\) на ось ox будет положительной, так как направление проекции силы сонаправлена с осью ox.
Не могу поверить я сам решил, черт это круто?
Очень рады Вашим успехам! Продолжайте в том же духе, у Вас всё получится!