Условие задачи:
С какой силой давит человек массой 70 кг на вертикальную спинку сиденья автомобиля, который движется по горизонтальному участку с ускорением 3 м/с2?
Задача №2.1.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=70\) кг, \(a=3\) м/с2, \(P-?\)
Решение задачи:
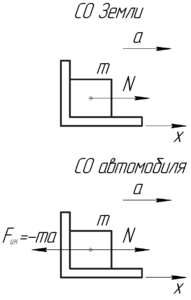 На рисунке покажем силы, действующие на тело. Получается, что на тело действует только одна реакция опоры \(N\), которая численно равна искомой силе давления \(P\) согласно третьему закону Ньютона (3ЗН).
На рисунке покажем силы, действующие на тело. Получается, что на тело действует только одна реакция опоры \(N\), которая численно равна искомой силе давления \(P\) согласно третьему закону Ньютона (3ЗН).
\[P = N\]
Из второго закона Ньютона следует:
\[N = ma\]
Тогда понятно, что:
\[P = ma\]
Посчитаем численно силу давления \(P\).
\[P = 70 \cdot 3 = 210\; Н\]
Хотелось бы сделать замечания к этой задаче. Непонятно откуда взялась реакция опоры \(N\) (особенно если рассматривать систему отсчета (СО), связанную с автомобилем), если вдоль этого направления не действует больше других сил. Но все станет на свои места, если заметить, что автомобиль не является инерциальной системой отсчета, так как он движется с ускорением. В этой СО человек покоится, а влияние ускорения автомобиля компенсируется силой инерции \({F_{ин}} = — ma\), где знак «минус» показывает направление, которое противоположно направлению ускорения. Тогда понятно, что реакция \(N\) вызвана этой силой инерции \({F_{ин}}\).
Ответ: 210 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.7 Определить вес человека массой 70 кг в лифте, опускающемся равнозамедленно
2.1.9 К нити подвешен груз массой 1 кг. Определить силу натяжения нити, если нить
2.1.10 К нити подвешен груз массой 1 кг, который опускается с ускорением 5 м/с2
А почему Вы отсчитываете реакцию опоры от человека, а не от опоры?
Получается,если учитывать машину как систему отсчета, мы бы учли в задаче ускорение и получили бы m*(g-a) => 70*(10-3)=490 ? Объясните физический смысл.
Нет, Вы бы получили то же самое равенство \(N=ma\).
Давление на сиденье в СО автомобиля можно объяснить действующей на человека силой инерции.
Если Вы плохо справляетесь со школьной динамикой, очень не рекомендую лезть в такую тему, как неинерциальные системы отсчета. Всему своё время)