Условие задачи:
С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются, пройдя по горизонтали путь 35 м от основания горы. Найти коэффициент трения.
Задача №2.3.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(H=2\) м, \(L=5\) м, \(S=35\) м, \(\mu-?\)
Решение задачи:
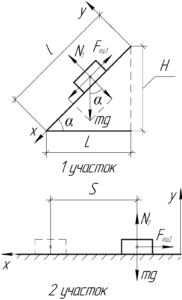Решать эту задачу будем, используя закон сохранения энергии. Согласно этому закону, работа силы трения равна изменению полной механической энергии.
\[A = \Delta E\;\;\;\;(1)\]
Когда санки в конце концов остановятся, то их полная механическая энергии станет равной нулю, хотя в начале они имели потенциальную энергию \(mgH\). Изменение энергии \(\Delta E\) равно:
\[\Delta E = 0 – mgH\]
Так как сила трения принимает разные значения при движении саней по горе и горизонтальной поверхности, то работу будем находить как сумму работ:
\[A = {A_1} + {A_2}\]
Таким образом равенство (1) примет такой вид:
\[{A_1} + {A_2} = – mgH\;\;\;\;(2)\]
Рассмотрим участок движения по горе. Из первого закона Ньютона в проекции на ось \(y\) найдем силу реакции опоры:
\[{N_1} = mg \cdot \cos \alpha \]
Тогда сила трения скольжения на этому участке равна:
\[{F_{тр1}} = \mu N_1\]
\[{F_{тр1}} = \mu mg \cdot \cos \alpha \]
Работа силы трения отрицательна, так как сила направлена против перемещения, и равна:
\[{A_1} = – {F_{тр1}} \cdot l\]
\[{A_1} = – \mu mg \cdot l \cdot \cos \alpha \]
Интересно, но из прямоугольного треугольника следует, что:
\[L = l \cdot \cos \alpha \]
Тогда:
\[{A_1} = – \mu mgL\;\;\;\;(3)\]
Аналогично определим работу силы трения на участке движения по горизонтальной поверхности, объяснения опустим.
\[{N_2} = mg\]
\[{F_{тр2}} = \mu mg\]
\[{A_2} = – {F_{тр2}} \cdot S\]
\[{A_2} = – \mu mg \cdot S\;\;\;\;(4)\]
Подставим (3) и (4) в (2), тогда:
\[ – \mu mg \cdot L – \mu mg \cdot S = – mgH\]
Сократим обе части равенства на \(mg\) и домножим на (-1), далее уже выразим искомый коэффициент \(\mu\).
\[\mu = \frac{H}{{L + S}}\]
Вычислим ответ:
\[\mu = \frac{2}{{5 + 35}} = 0,05\]
Ответ: 0,05.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.15 С каким ускорением движутся грузы m1=0,5 кг и m2=0,6 кг, если высота наклонной
2.3.17 Чему должен быть равен минимальный коэффициент трения между шинами
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
Всё идеально, а главное понятно)
Спасибо
Отлично, что я нашёл ответ на задачу
что значит долгое тире?
Знак “минус”, если правильно понял Ваш вопрос
А почему L =l*cos a а например не синус почему написано что это следует из прямоугольного треугольника из него следует только что L^2=l^2-h^2 обьясните пожалуйста
Потому в указанном прямоугольном треугольнике l – гипотенуза, а L – прилежащий к углу α катет, поэтому там косинус, а не синус
А почему в этом равенстве
A1=—μmgL за расстояние берется L, если должно быть l?
Невнимательно читаете решение, вообще я пишу, что:
A1 = – μmg*l*cos a
Из рисунка хорошо видно, что:
L=l*cos a
Собственно поэтому и имеем:
A1 = – μmg*L
У меня появился единственный вопрос. Почему при решении этой задачи мы принебрегаем силой тяжести. Ведь оно тоже справоцирует скорость с силой mgsin@
Я решал задачу исходя из закона сохранения энергии, согласно которому изменение полной механической энергии равно работе неконсервативных сил, действующих в системе. В данном случае действует только одна неконсервативная сила – сила трения скольжения. Работа силы тяжести учтена в изменении полной механической энергии (то самое \(mgH\) в решении).