Условие задачи:
Пуля массой 9 г, летевшая со скоростью 600 м/с, попадает в деревянную стену и проникает в нее на глубину 20 см. Определить среднюю силу сопротивления движению пули.
Задача №2.1.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=9\) г, \(\upsilon=600\) м/с, \(S=20\) см, \(F-?\)
Решение задачи:
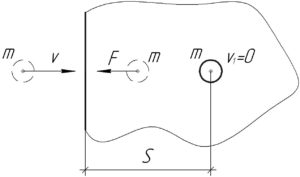Применим теорему об изменении кинетической энергии (закон сохранения энергии):
\[A = 0 – \frac{{m{\upsilon ^2}}}{2}\]
В этом выражении \(A\) – это работа сила сопротивления. Её определяют как скалярное произведение вектора самой силы и вектор перемещения. Так как они направлены в противоположные стороны (угол между ними 180°), то:
\[A = \overrightarrow F \cdot \overrightarrow S = F \cdot S \cdot \cos 180^\circ = – FS\]
В итоге:
\[ – FS = – \frac{{m{\upsilon ^2}}}{2} \Rightarrow F = \frac{{m{\upsilon ^2}}}{{2S}}\]
Переведем некоторые величины в систему СИ.
\[9\; г = \frac{9}{{1000}}\; кг = 0,009\; кг\]
\[20\; см = \frac{{20}}{{100}}\; м = 0,2\; м\]
Посчитаем ответ.
\[F = \frac{{0,009 \cdot {{600}^2}}}{{2 \cdot 0,2}} = 8100\; Н = 8,1\; кН\]
Ответ: 8,1 кН.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.27 Пуля массой 10 г, летевшая со скоростью 400 м/с, пробив доску толщиной 5 см
2.1.29 На тело, движущееся по горизонтальной поверхности, действуют следующие силы
2.1.30 На участке дороги, где для автотранспорта установлена предельная скорость 30 км/ч