Условие задачи:

Пуля массой 10 г подлетает к доске массой 1 кг со скоростью 600 м/с и, пробив ее в центре, вылетает со скоростью 400 м/с. Какая доля потерянной кинетической энергии пули пошла на кинетическую энергию доски?

Задача №2.8.42 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) г, \(M=1\) кг, \(\upsilon_0=600\) м/с, \(\upsilon=400\) м/с, \(\frac{E_д}{\Delta E_п}-?\)

Решение задачи:

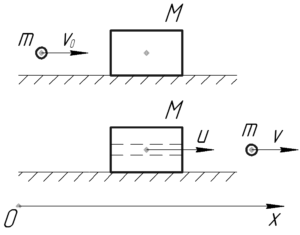Применим закон сохранения импульса для момента непосредственно перед и сразу после пробивания доски пулей:

\[m{\upsilon _0} = m\upsilon  + Mu\]

В этом равенстве одно неизвестное — это скорость доски \(u\), выразим её:

\[u = \frac{{m\left( {{\upsilon _0} — \upsilon } \right)}}{M}\]

Кинетическая энергия доски после прохождения через неё пули равна:

\[{E_д} = \frac{{M{u^2}}}{2}\]

\[{E_д} = \frac{{M{m^2}{{\left( {{\upsilon _0} — \upsilon } \right)}^2}}}{{2{M^2}}} = \frac{{{m^2}{{\left( {{\upsilon _0} — \upsilon } \right)}^2}}}{{2M}}\]

Потерянная кинетическая энергия пули, очевидно, равна:

\[\Delta {E_п} = \frac{{m\upsilon _0^2}}{2} — \frac{{m{\upsilon ^2}}}{2}\]

\[\Delta {E_п} = \frac{{m\left( {\upsilon _0^2 — {\upsilon ^2}} \right)}}{2}\]

В итоге искомое отношение кинетической энергии доски к потерянной кинетической энергии пули равно:

\[\frac{{{E_д}}}{{\Delta {E_п}}} = \frac{{{m^2}{{\left( {{\upsilon _0} — \upsilon } \right)}^2} \cdot 2}}{{2M \cdot m\left( {\upsilon _0^2 — {\upsilon ^2}} \right)}}\]

\[\frac{{{E_д}}}{{\Delta {E_п}}} = \frac{{m{{\left( {{\upsilon _0} — \upsilon } \right)}^2}}}{{M\left( {\upsilon _0^2 — {\upsilon ^2}} \right)}}\]

Переведем массу пули в систему СИ:

\[10\; г = \frac{{10}}{{1000}}\; кг = 0,01\; кг\]

Подставим численные данные в последнюю формулу и посчитаем ответ.

\[\frac{{{E_д}}}{{\Delta {E_п}}} = \frac{{0,01 \cdot {{\left( {600 — 400} \right)}^2}}}{{1 \cdot \left( {{{600}^2} — {{400}^2}} \right)}} = 0,002\]

Ответ: 0,002.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту
2.8.43 Тело скользит вниз по наклонной плоскости, плавно переходящей в вертикальную
2.8.44 В школьном опыте с «мертвой петлей» шарик массой 0,1 кг отпущен с высоты h=3R