Условие задачи:
Пуля, летящая горизонтально со скоростью 510 м/с, попадает в ящик, лежащий на горизонтальной поверхности, и, пробив ящик, вылетает в том же направлении со скоростью 10 м/с. Какое расстояние пройдет ящик? Коэффициент трения между ящиком и поверхностью равен 0,1, масса ящика 10 кг, масса пули 10 г.
Задача №2.8.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\upsilon_0=510\) м/с, \(\upsilon=10\) м/с, \(\mu=0,1\), \(M=10\) кг, \(m=10\) г, \(S-?\)
Решение задачи:
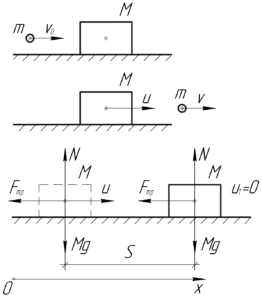 На систему тел «пуля-ящик» вдоль горизонтальной оси \(x\) в момент до пробивания ящика и сразу после этого не действуют никакие силы, значит импульс тел вдоль этой оси должен сохраняться. Запишем закон сохранения импульса в проекции на ось \(x\):
На систему тел «пуля-ящик» вдоль горизонтальной оси \(x\) в момент до пробивания ящика и сразу после этого не действуют никакие силы, значит импульс тел вдоль этой оси должен сохраняться. Запишем закон сохранения импульса в проекции на ось \(x\):
\[m{\upsilon _0} = Mu + m\upsilon \]
Здесь \(u\) — скорость ящика после прохождения через него пули. Выразим её:
\[u = \frac{{m\left( {{\upsilon _0} — \upsilon } \right)}}{M}\;\;\;\;(1)\]
Далее воспользуемся теоремой об изменении кинетической энергии тела, согласно которой работа некоторой силы равна изменению кинетической энергии тела:
\[A = \Delta {E_к}\;\;\;\;(2)\]
На тело действует лишь одна сила, которая после приобретения ящиком скорости будет совершать работу — это сила трения скольжения. Её можно определить по следующей формуле:
\[{F_{тр}} = \mu N = \mu Mg\]
Работа силы трения скольжения равна:
\[A = — F \cdot S = — \mu MgS\;\;\;\;(3)\]
Сила тяжести и сила реакции опоры работу в данном случае не совершают, так как они перпендикулярны перемещению.
Ящик в конце концов остановится, значит изменение его кинетической энергии равно:
\[\Delta {E_к} = 0 — \frac{{M{u^2}}}{2}\;\;\;\;(4)\]
Подставим выражения (3) и (4) в (2):
\[ — \mu MgS = 0 — \frac{{M{u^2}}}{2}\]
\[\mu MgS = \frac{{M{u^2}}}{2}\]
\[S = \frac{{{u^2}}}{{2\mu g}}\]
Подставим в последнюю формулу выражение (1), тогда мы получим решение задачи в общем виде:
\[S = \frac{{{m^2}{{\left( {{\upsilon _0} — \upsilon } \right)}^2}}}{{2\mu g{M^2}}}\]
Переведем массу пули в систему СИ, далее подставим все величины в итоговую формулу и посчитаем ответ.
\[10\; г = \frac{{10}}{{1000}}\; кг = 0,01\; кг\]
\[S = \frac{{{{0,01}^2}{{\left( {510 — 10} \right)}^2}}}{{2 \cdot 0,1 \cdot 10 \cdot {{10}^2}}} = 0,125\; м = 12,5\; см\]
Ответ: 12,5 см.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.8.25 На тело массой 1 кг, брошенное с поверхности Земли вертикально вверх с начальной
2.8.27 Для откачки воды из шахты глубиной 20 м поставлен насос с двигателем мощностью
2.8.28 Какую работу надо совершить, чтобы поставить однородный куб массой 10 кг
Решите пожалуйста задачу!
Условие:
шарик влетает в ящик с песком под углом альфа и застревает в нем. У шарика есть скорость V и масса m. Ящик стоит на плоской поверхности, масса ящика M, есть коэффициент трения мю между ящиком и поверхностью. Найти скорость ящика после удара шарика. Преподаватель дал подсказку решать через 2 закон Ньютона в импульсной форме. Напишите пояснения к КАЖДОМУ действию.
Можно проще