Решение: На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения

Условие задачи:

На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения уменьшилась в 100 раз?

Задача №2.5.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

$\frac{F_{т1}}{F_{т2}}=100$ , $h-?$

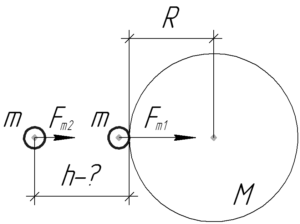Из закона всемирного тяготения следует, что сила тяготения вблизи поверхности Земли равна:

${F_{т1}} = G\frac{{Mm}}{{{R^2}}}\;\;\;\;(1)$

В этой формуле $G$ — гравитационная постоянная, $M$ — масса Земли, $R$ — радиус Земли, а $m$ — масса некоторого тела.

Из того же закона всемирного тяготения следует, что силу тяготения на некоторой высоте $h$ можно определить по формуле:

${F_{т2}} = G\frac{{Mm}}{{{{\left( {R + h} \right)}^2}}}\;\;\;\;(2)$

По условию $\frac{F_{т1}}{F_{т2}}=100$ , поэтому поделив правые части формул (1) и (2) друг на друга, получим:

$\frac{{{{\left( {R + h} \right)}^2}}}{{{R^2}}} = 100$

$\frac{{R + h}}{R} = 10$

$R + h = 10R$

$h = 9R$

Радиус Земли $R$ можно узнать, посмотрев таблицы в конце любого сборника по физике — он равен 6,4·10⁶ м.

Численно ответ равен:

$h = 9 \cdot 6,4 \cdot {10^6} = 57,6 \cdot {10^6}\;м = 57600\;км$

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.