Условие задачи:
Металлический шарик массой 100 г падает на горизонтальную плоскость с высоты 20 см и отскакивает после удара снова на высоту 20 см. Найти среднюю силу удара шарика о плоскость, если длительность удара 0,04 с.
Задача №2.1.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m=100\) г, \(h=20\) см, \(\Delta t=0,04\) с, \(F-?\)
Решение задачи:
Кликните по схеме, чтобы её увеличить.
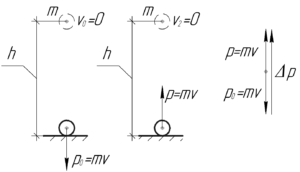Тот факт, что шарик вернулся после отскока от плоскости на ту же высоту, говорит о том, что удар шарика о плоскость был абсолютно упругий, т.е. потерь скорости не было.
Саму силу удара определим благодаря второму закону Ньютона, записанному в общем виде:
\[F = \frac{{\Delta p}}{{\Delta t}}\;\;\;\;(1)\]
Если посмотреть на правую часть представленного рисунка, то видно, что изменение импульса по модулю равно:
\[\Delta p = 2m\upsilon \;\;\;\;(2)\]
Здесь \(\upsilon\) — это скорость шарика в момент непосредственного касания с плоскостью. Её можно определить, использовав следующую известную формулу:
\[{\upsilon ^2} — \upsilon _0^2 = 2aS\]
Так как шарик бросали без начальной скорости (\(\upsilon_0=0\)), ускорение шарика \(a\) равно ускорению свободного падения \(g\), а модуль перемещения \(S\) равен высоте \(h\), с которой бросали шарик, то данное выражение примет вид.
\[{\upsilon ^2} = 2gh\]
\[\upsilon = \sqrt {2gh} \;\;\;\;(3)\]
Подставим выражение (3) в (2), а полученное в (1).
\[F = \frac{{2m\sqrt {2gh} }}{{\Delta t}}\]
Переведем некоторые величины в систему СИ.
\[100\; г = \frac{{100}}{{1000}}\; кг = 0,1\; кг\]
\[20\; см = \frac{{20}}{{100}}\; м = 0,2\; м\]
Дело остается за малым, считаем ответ.
\[F = \frac{{2 \cdot 0,1 \cdot \sqrt {2 \cdot 10 \cdot 0,2} }}{{0,04}} = 10\; Н\]
Ответ: 10 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.35 Летящая пуля попадает в мешок с песком и углубляется на 15 см. На какую глубину
2.1.37 Мяч массой 0,15 кг ударяется о гладкую стенку под углом 30 градусов к ней
2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2mv получилось потому что (mv-(-mv))=2mv?
Скажите , а правильно , что 2mv получается посредством выражения: (mv-(-mv))? То есть одинаковые импульсы, но направленные в разные стороны.
Разве там не должно быть ещё +mg?
Где там? Не дожидаясь ответа на свой вопрос, отвечу на Ваш — нет, не должно быть.
почему изменение испульса 2mv? рисунок мне ничего не говорит
Изменение импульса (как и сам импульс) — величина векторная. На правой части представленного рисунка показаны начальный и конечный векторы. Если Вы умеете находить разность векторов, то при вычитании векторов получите вектор изменения импульса, равный по модулю 2mv.
обьясните пожалуйста как складывать и вычитать вектора с таких задачах
Вектора складываются и вычитаются как обычно в математике, правила элементарные (причем правило вычитания выходит из правила сложения), посмотрите в учебнике геометрии.