Условие задачи:
Каково ускорение свободного падения на поверхности Солнца, если радиус Солнца в 108 раз больше радиуса Земли, а плотность в 4 раза меньше плотности Земли? (\(g=9,8\) м/с2)
Задача №2.5.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R_с=108R_з\), \(\rho_с=0,25\rho_з\), \(g_з=9,8\) м/с2, \(g_с-?\)
Решение задачи:
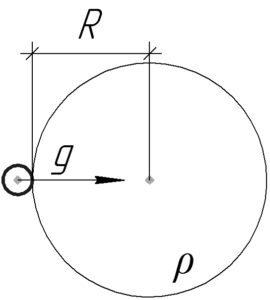Давайте узнаем как зависит ускорение свободного падения на поверхности некоторой планеты от её средней плотности и радиуса, для этого запишем формулу его определения:
\[g = G\frac{M}{{{R^2}}}\;\;\;\;(1)\]
Массу планеты можно найти из её средней плотности \(\rho\) и объема \(V\):
\[M = \rho \cdot V\;\;\;\;(2)\]
Планеты обычно имеют форму, близкую к шарообразной, поэтому объем \(V\) можно посчитать по следующей формуле:
\[V = \frac{4}{3}\pi {R^3}\;\;\;\;(3)\]
Подставим выражения (2) и (3) в формулу (1), тогда:
\[g = G\frac{{4\rho \cdot \pi {R^3}}}{{3{R^2}}} = \frac{4}{3}\pi G\rho R\]
Видно, что ускорение свободного падения вблизи поверхности некоторой планеты зависит линейно от средней плотности и радиуса планеты. Учитывая это, ускорения свободного падения на Земли и на Солнце можно определить по следующим формулам:
\[\left\{ \begin{gathered}
g_c = \frac{4}{3}G\pi \rho_с R_с \hfill \\
g_з = \frac{4}{3}G\pi \rho_з R_з \hfill \\
\end{gathered} \right.\]
Разделим верхнее равенство на нижнее:
\[\frac{{{g_с}}}{{{g_з}}} = \frac{{{\rho _с}{R_с}}}{{{\rho _з}{R_з}}}\]
Поэтому:
\[g_с = g_з\frac{{{\rho _с}{R_с}}}{{{\rho _з}{R_з}}}\]
Так как в условии сказано, что \(R_с=108R_з\) и \(\rho_с=0,25\rho_з\), то:
\[g_с = g_з\frac{{0,25{\rho _з} \cdot 108{R_з}}}{{{\rho _з}{R_з}}} = 27g_з\]
Осталось посчитать численный ответ:
\[g = 27 \cdot 9,8 = 264,6\; м/с^2\]
Ответ: 264,6 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.5.4 Искусственный спутник Земли движется на высоте 12800 км. Найти скорость движения
2.5.6 На какое расстояние от поверхности Земли нужно удалить тело, чтобы сила тяготения
2.5.7 Определить первую космическую скорость для планеты, масса и радиус которой в два
Такое большое ускорение свободного падения вблизи поверхности Солнца означает, что тело будет очень сильно притягиваться к поверхности и тело будет двигаться очень быстро?
Да, только правильно говорить, что:
1) притягиваться к Солнцу (а не к поверхности);
2) тело будет быстро ускоряться, а не двигаться быстро (если сравнивать с Землей, естественно).
Как вы выразили g Солнца?
Разделил верхнее равенство на нижнее (смотрите решение, я его дополнил, чтобы стало понятнее)
а куда пи ушло,с чем оно сократилось?
Решение поправлено, спасибо за замечание (потеряли число пи).