Условие задачи:

Горизонтально летящая пуля массой 10 г насквозь пробивает первоначально покоившийся шар массой 50 г и вылетает со скоростью, вдвое меньшей первоначальной. Какая доля кинетической энергии пули превратилась во внутреннюю энергию?

Задача №2.8.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=10\) г, \(M=50\) г, \(\upsilon=\frac{\upsilon_0}{2}\), \(\frac{Q}{E}-?\)

Решение задачи:

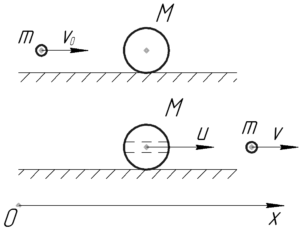Так как какая-то часть кинетической энергии превращается во внутреннюю энергию, значит имеет место неупругий удар. Запишем закон сохранения энергии и закон сохранения импульса для моментов до и после удара:

\[\left\{ \begin{gathered}
\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + \frac{{M{u^2}}}{2} + Q \;\;\;\;(1)\hfill \\
m{\upsilon _0} = m\upsilon + Mu \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]

Так как по заданию известно, что \(\upsilon=\frac{\upsilon_0}{2}\), то выражение (2) примет вид:

\[m{\upsilon _0} = m\frac{{{\upsilon _0}}}{2} + Mu\]

\[m\frac{{{\upsilon _0}}}{2} = Mu\]

\[u = \frac{{m{\upsilon _0}}}{{2M}}\]

Полученное выражения для скорости шара после удара \(u\) и данное в условии \(\upsilon=\frac{\upsilon_0}{2}\) подставим в (1).

\[\frac{{m\upsilon _0^2}}{2} = \frac{{m\upsilon _0^2}}{{2 \cdot 4}} + \frac{M}{2}{\left( {\frac{{m{\upsilon _0}}}{{2M}}} \right)^2} + Q\]

\[\frac{{3m\upsilon _0^2}}{8} = \frac{{{m^2}\upsilon _0^2}}{{8M}} + Q\]

\[Q = \frac{{m\upsilon _0^2}}{2}\left( {\frac{3}{4} — \frac{m}{{4M}}} \right)\]

Так как начальная кинетическая энергия пули равна \(E = \frac{{m\upsilon _0^2}}{2}\), то искомое отношение равно:

\[\frac{Q}{E} = \left( {\frac{3}{4} — \frac{m}{{4M}}} \right)\]

Переведем массы пули и шара в систему СИ:

\[10\; г = \frac{{10}}{{1000}}\; кг = 0,01\; кг\]

\[50\; г = \frac{{50}}{{1000}}\; кг = 0,05\; кг\]

Посчитаем численный ответ к этой задаче:

\[\frac{Q}{E} = \left( {\frac{3}{4} — \frac{{0,01}}{{4 \cdot 0,05}}} \right) = 0,7\]

Ответ: 0,7.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.8.38 Пуля массой 9 г, летевшая вертикально вверх со скоростью 200 м/с, пробила
2.8.40 На вершине шара радиусом 30 см лежит небольшая шайба. После легкого толчка
2.8.41 Определите время подъема камня массой 1 кг, брошенного под углом к горизонту