Решение: Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность

Условие задачи:

Гирька массой 0,1 кг, привязанная легкой нерастяжимой нитью, описывает окружность в вертикальной плоскости. Скорости гирьки в верхней и нижней частях траектории равны 4 и 6 м/с, соответственно. Определить натяжение нити в верхней точке траектории.

Задача №2.4.16 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=0,1\) кг, \(\upsilon_в=4\) м/с, \(\upsilon_н=6\) м/с, \(T-?\)

Решение задачи:

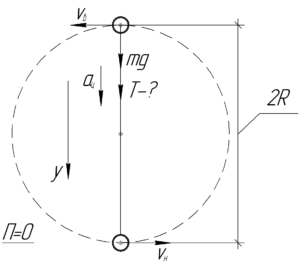Изобразим на схеме гирьку в верхней и нижней точках траектории. Покажем все силы, действующие на гирьку в верхней точке траектории. Применим второй закон Ньютона в проекции на ось \(y\):

\[T + mg = m{a_ц}\]

\[T = m\left( {{a_ц} — g} \right)\]

Радиус описываемой гирькой окружности равен радиусу кривизны траектории гирьки, что очевидно. Так как скорость гирьки в верхней точке равна \(\upsilon_в\), то ускорение \(a_ц\) можно найти по формуле:

\[{a_ц} = \frac{{\upsilon _в^2}}{R}\]

\[T = m\left( {\frac{{\upsilon _в^2}}{R} — g} \right)\;\;\;\;(1)\]

Так как неконсервативные силы отсутствуют, то применим закон сохранения энергии, выбрав нуль потенциальной энергии на уровне нижней точки траектории гирьки.

\[\frac{{m\upsilon _н^2}}{2} = \frac{{m\upsilon _в^2}}{2} + mg \cdot 2R\]

Откуда выразим неизвестный радиус \(R\):

\[R = \frac{{\upsilon _н^2 — \upsilon _в^2}}{{4g}}\]

Формула (1) станет теперь такой:

\[T = m\left( {\frac{{4g\upsilon _в^2}}{{\upsilon _н^2 — \upsilon _в^2}} — g} \right)\]

Считаем ответ:

\[T = 0,1 \cdot \left( {\frac{{4 \cdot 10 \cdot {4^2}}}{{{6^2} — {4^2}}} — 10} \right) = 2,2\; Н\]