Условие задачи:
Два шарика массами 2 и 3 г движутся в горизонтальной плоскости со скоростями 6 и 4 м/с, соответственно. Направления движения шариков составляют угол 90°. Шарики неупруго соударяются. Какое количество теплоты при этом выделяется?
Задача №2.10.32 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(m_1=2\) г, \(m_2=3\) г, \(\upsilon_1=6\) м/с, \(\upsilon_2=4\) м/с, \(Q-?\)
Решение задачи:
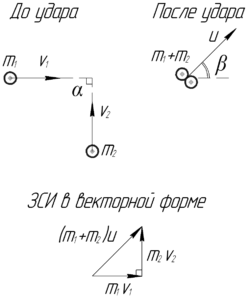 При любом ударе — упругом и неупругом — всегда можно применять закон сохранения импульса (ЗСИ). Запишем его в векторной форме:
При любом ударе — упругом и неупругом — всегда можно применять закон сохранения импульса (ЗСИ). Запишем его в векторной форме:
\[\overrightarrow {{m_1}{\upsilon _1}} + \overrightarrow {{m_2}{\upsilon _2}} = \overrightarrow {\left( {{m_1} + {m_2}} \right)u} \]
Так как между угол между векторами скоростей (а значит и импульсов) равен 90°, то применим теорему Пифагора, и получим такое равенство:
\[m_1^2\upsilon _1^2 + m_2^2\upsilon _2^2 = {\left( {{m_1} + {m_2}} \right)^2}{u^2}\]
Выразим из него квадрат скорости \(u\) после удара, оно нам ещё пригодится:
\[{u^2} = \frac{{m_1^2\upsilon _1^2 + m_2^2\upsilon _2^2}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\;\;\;\;(1)\]
Также запишем закон сохранения энергии, при этом обязательно учтем, что часть энергии перейдёт в теплоту \(Q\):
\[\frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} = \frac{{\left( {{m_1} + {m_2}} \right){u^2}}}{2} + Q\].
Оставив искомое количество теплоты \(Q\) в одной стороне, перенесем все остальные члены в другую.
\[Q = \frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} — \frac{{\left( {{m_1} + {m_2}} \right){u^2}}}{2}\]
Подставим в эту формулу выражение (1) и приведем всё под общий знаменатель.
\[Q = \frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} — \frac{{\left( {{m_1} + {m_2}} \right)}}{2} \cdot \frac{{m_1^2\upsilon _1^2 + m_2^2\upsilon _2^2}}{{{{\left( {{m_1} + {m_2}} \right)}^2}}}\]
\[Q = \frac{{{m_1}\upsilon _1^2}}{2} + \frac{{{m_2}\upsilon _2^2}}{2} — \frac{{m_1^2\upsilon _1^2 + m_2^2\upsilon _2^2}}{{2\left( {{m_1} + {m_2}} \right)}}\]
\[Q = \frac{{{m_1}\upsilon _1^2\left( {{m_1} + {m_2}} \right) + {m_2}\upsilon _2^2\left( {{m_1} + {m_2}} \right) — m_1^2\upsilon _1^2 — m_2^2\upsilon _2^2}}{{2\left( {{m_1} + {m_2}} \right)}}\]
\[Q = \frac{{m_1^2\upsilon _1^2 + {m_1}{m_2}\upsilon _1^2 + {m_1}{m_2}\upsilon _2^2 + m_2^2\upsilon _2^2 — m_1^2\upsilon _1^2 — m_2^2\upsilon _2^2}}{{2\left( {{m_1} + {m_2}} \right)}}\]
\[Q = \frac{{{m_1}{m_2}\upsilon _1^2 + {m_1}{m_2}\upsilon _2^2}}{{2\left( {{m_1} + {m_2}} \right)}}\]
После всех преобразований мы получили такую конечную формулу:
\[Q = \frac{{{m_1}{m_2}\left( {\upsilon _1^2 + \upsilon _2^2} \right)}}{{2\left( {{m_1} + {m_2}} \right)}}\]
Переведем массы шариков в систему СИ:
\[2\; г = \frac{2}{{1000}}\; кг = 2 \cdot {10^{ — 3}}\; кг\]
\[3\; г = \frac{3}{{1000}}\; кг = 3 \cdot {10^{ — 3}}\; кг\]
Теперь посчитаем ответ к задаче:
\[Q = \frac{{2 \cdot {{10}^{ — 3}} \cdot 3 \cdot {{10}^{ — 3}} \cdot \left( {{6^2} + {4^2}} \right)}}{{2\left( {2 \cdot {{10}^{ — 3}} + 3 \cdot {{10}^{ — 3}}} \right)}} = 0,0312\; Дж = 31,2\; мДж\]
Ответ: 31,2 мДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.10.31 Человек массой 80 кг захотел спуститься по веревочной лестнице из свободно
2.10.33 Космический корабль на скорости 10 км/с попадает в неподвижное облако
2.10.34 На горизонтальной плоскости сделан выстрел из винтовки, ствол которой направлен