Условие задачи:

Два шара массами 0,3 и 0,2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с, второго — 2,5 м/с. Сколько энергии превратилось в тепло после абсолютно неупругого удара шаров?

Задача №2.10.6 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(M=0,3\) кг, \(m=0,2\) кг, \(\upsilon_0=5\) м/с, \(u_0=2,5\) м/с, \(Q-?\)

Решение задачи:

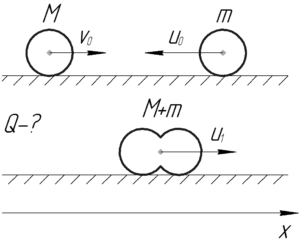Так как на систему «шар \(M\) — шар \(m\)» вдоль оси \(x\) не действуют никакие силы, то эта система замкнута вдоль этой оси. Исходя из этого, запишем закон сохранения импульса в проекции на эту ось:

\[M{\upsilon _0} — m{u_0} = \left( {M + m} \right){u_1}\]

Выразим скорость тел \(u_1\) после удара:

\[{u_1} = \frac{{M{\upsilon _0} — m{u_0}}}{{M + m}}\;\;\;\;(1)\]

Также запишем закон сохранения энергии, при этом не забудем учесть, что часть энергии после абсолютно неупругого удара перейдет в тепло \(Q\):

\[\frac{{M\upsilon _0^2}}{2} + \frac{{mu_0^2}}{2} = \frac{{\left( {M + m} \right)u_1^2}}{2} + Q\]

Оставим \(Q\) в одной стороне, остальное перенесем в другую:

\[Q = \frac{{M\upsilon _0^2}}{2} + \frac{{mu_0^2}}{2} — \frac{{\left( {M + m} \right)u_1^2}}{2}\]

Подставим (1) в последнюю формулу:

\[Q = \frac{{M\upsilon _0^2}}{2} + \frac{{mu_0^2}}{2} — \frac{{\left( {M + m} \right)}}{2} \cdot \frac{{{{\left( {M{\upsilon _0} — m{u_0}} \right)}^2}}}{{{{\left( {M + m} \right)}^2}}}\]

\[Q = \frac{{M\upsilon _0^2}}{2} + \frac{{mu_0^2}}{2} — \frac{{{{\left( {M{\upsilon _0} — m{u_0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Приведем под общий знаменатель:

\[Q = \frac{{M\upsilon _0^2\left( {M + m} \right) + mu_0^2\left( {M + m} \right) — {{\left( {M{\upsilon _0} — m{u_0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Раскроем скобки в числителе:

\[Q = \frac{{{M^2}\upsilon _0^2 + mM\upsilon _0^2 + mMu_0^2 + {m^2}u_0^2 — {M^2}\upsilon _0^2 + 2mM{\upsilon _0}{u_0} — {m^2}u_0^2}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM\upsilon _0^2 + mMu_0^2 + 2mM{\upsilon _0}{u_0}}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM\left( {\upsilon _0^2 + 2{\upsilon _0}{u_0} + u_0^2} \right)}}{{2\left( {M + m} \right)}}\]

\[Q = \frac{{mM{{\left( {{\upsilon _0} + {u_0}} \right)}^2}}}{{2\left( {M + m} \right)}}\]

Как Вы видите, получилась очень «красивая» формула. Посчитаем численный ответ к задаче.

\[Q = \frac{{0,2 \cdot 0,3 \cdot {{\left( {5 + 2,5} \right)}^2}}}{{2\left( {0,3 + 0,2} \right)}} = 3,375\; Дж\]

Ответ: 3,375 Дж.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.10.5 Шары массами 1 и 2 кг движутся навстречу друг другу. Скорость первого шара 5 м/с
2.10.7 Охотник стреляет с легкой надувной лодки, находящейся в покое. Какую скорость
2.10.8 Груз массой 0,5 кг падает с некоторой высоты на плиту массой 1 кг, укрепленную