Условие задачи:

Два автомобиля с одинаковыми массами \(m\) движутся со скоростями \(\upsilon\) и \(2 \upsilon\) относительно Земли навстречу друг другу. Чему равен модуль импульса второго автомобиля в системе отсчета, связанной с первым автомобилем?

Задача №2.1.39 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m\), \(\upsilon\), \(2 \upsilon\), \(p_{21}-?\)

Решение задачи:

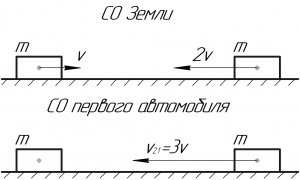Перейдем в систему отсчета (СО), связанную с первым автомобилем. Чтобы узнать скорость второго автомобиля в этой СО, к вектору его скорости (в СО Земли) необходимо прибавить вектор, равный по величине, но противоположный по направлению вектору скорости первого автомобиля (смотри схему). Модуль скорости второго автомобиля в СО первого автомобиля, очевидно, равен:

\[{\upsilon _{21}} = 2\upsilon  + \upsilon  = 3\upsilon \]

Тогда модуль его импульса равен:

\[{p_{21}} = m{\upsilon _{21}} = 3m\upsilon \]

Запомните, что импульс — это относительная величина, его значение зависит от выбора системы отсчета!

Ответ: \(3m\upsilon\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.38 Вор, масса которого вместе с добычей 125 кг, убегая, налетает на камень. Столкновение
2.1.40 Две стальные проволоки одинаковой длины, диаметр первой в 3 раза больше
2.1.41 Ракета на старте с поверхности Земли движется вертикально вверх с ускорением