Условие задачи:
Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому горизонтальному столу под действием горизонтальной силы \(F\), приложенной к первому кубику. Чему равна сила натяжения нити, связывающей третий и четвертый кубики?
Задача №2.1.81 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(F\), \(T_3-?\)
Решение задачи:
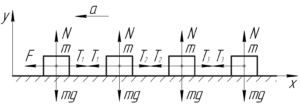 Так как кубики движутся по гладкому столу, то силой трения скольжения кубиков о стол можно пренебречь. Поскольку кубики одинаковые, то все они имеют одинаковую массу, обозначим её \(m\).
Так как кубики движутся по гладкому столу, то силой трения скольжения кубиков о стол можно пренебречь. Поскольку кубики одинаковые, то все они имеют одинаковую массу, обозначим её \(m\).
Понятно, что все кубики под действием силы \(F\) будут двигаться с одинаковым ускорением \(a\). На схеме покажем все силы, действующие на кубики, далее запишем второй закон Ньютона в проекции на ось \(x\) для всех кубиков.
\[\left\{ \begin{gathered}
F — {T_1} = ma \hfill \\
{T_1} — {T_2} = ma \hfill \\
{T_2} — {T_3} = ma \hfill \\
{T_3} = ma \hfill \\
\end{gathered} \right.\]
Сложим вместе все выражения системы, тогда получим:
\[F = 4ma \Rightarrow a = \frac{F}{{4m}}\]
Интересно, но это выражение можно получить гораздо проще, если вы знаете теорему о движении центра масс системы. Знать Вы её не обязаны, так как она не входит в курс школьной физики.
Отлично, мы определили ускорение, с которым движутся кубики. Подставим полученную формулу для ускорения в последнее выражение системы.
\[{T_3} = \frac{{Fm}}{{4m}} = \frac{F}{4}\]
Ответ: \(\frac{F}{4}\).
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.1.80 К невесомой нити подвешен груз массы 1 кг. Точка подвеса нити движется
2.1.82 Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной
2.1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
а есть какой-нибудь способ по проще решить задачку, а то вообще ничего не понятно
Задача очень простая, и решение очень простое
Учите матчасть, если не понимаете…