Условие задачи:
Автомобиль движется по выпуклому мосту радиусом 40 м. Какое максимальное ускорение в направлении движения может развить автомобиль в высшей точке, если скорость его в этой точке 50,4 км/ч, а коэффициент трения колес автомобиля о мост 0,6?
Задача №2.4.36 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(R=40\) м, \(\upsilon=50,4\) км/ч, \(\mu=0,6\), \(a-?\)
Решение задачи:
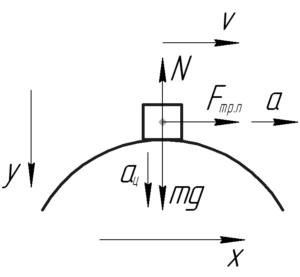 Между колесами автомобиля и дорогой действует сила трения покоя \(F_{тр.п}\). Заметьте, что сила трения именно покоя, а не скольжения, так как в противном случае колеса бы проскальзывали. Второй закон Ньютона в проекции на ось \(x\) даёт такое равенство:
Между колесами автомобиля и дорогой действует сила трения покоя \(F_{тр.п}\). Заметьте, что сила трения именно покоя, а не скольжения, так как в противном случае колеса бы проскальзывали. Второй закон Ньютона в проекции на ось \(x\) даёт такое равенство:
\[{F_{тр.п}} = ma\;\;\;\;(1)\]
Из него становится понятно, что автомобиль разовьёт максимальное ускорение, когда сила трения покоя достигнет своей максимальной величины. Максимальную силу трения покоя можно найти по той же формуле, что и силу трения скольжения:
\[{F_{тр.п}} = \mu N\;\;\;\;(2)\]
Приравняем (1) и (2), тогда получим:
\[ma = \mu N\]
\[a = \frac{{\mu N}}{m}\;\;\;\;(3)\]
Чтобы найти силу реакции опоры, запишем второй закон Ньютона в проекции на ось \(y\):
\[mg — N = m{a_ц}\]
Зная скорость автомобиля \(\upsilon\) и радиус выпуклого моста \(R\), легко найдем центростремительное ускорение \(a_ц\) по формуле:
\[{a_ц} = \frac{{{\upsilon ^2}}}{R}\]
\[mg — N = m\frac{{{\upsilon ^2}}}{R}\]
\[N = m\left( {g — \frac{{{\upsilon ^2}}}{R}} \right)\]
Полученное выражение для силы реакции опоры \(N\) подставим в формулу (3), в итоге имеем решение задачи в общем виде:
\[a = \mu \left( {g — \frac{{{\upsilon ^2}}}{R}} \right)\]
Переведем скорость автомобиля в систему СИ:
\[50,4\; км/ч = \frac{{50,4 \cdot 1000}}{{1 \cdot 3600}}\; м/с = \frac{{504}}{{36}}\; м/с = 14\; м/с\]
Посчитаем ответ:
\[a = 0,6 \cdot \left( {10 — \frac{{{{14}^2}}}{{40}}} \right) = 3,06\; м/с^2\]
Ответ: 3,06 м/с2.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.4.35 Чаша в форме полусферы радиусом 0,8 м вращается с постоянной угловой скоростью
2.4.37 Тело массой 0,1 кг вращается в вертикальной плоскости на нити длиной 1 м. Ось
2.4.38 На горизонтально расположенном диске, вращающемся с частотой 60 об/мин, помещают
Как мы получили формулу на ось y?
Подскажите пожалуйста ход решения.
Автомобиль занесло на горизонтальном повороте дороги радиусом кривизны R = 200 м.
Было ограничение скорости до 40 км / ч. На сколько км / ч превышена скорость? Коэффициент трения между шинами и дорогой составил f = 0,8.
У меня получается V = √0,8*9,8*200 = 39,59 что явно неверно
Почему неверно? Вы ответ получили в м/с (а ограничение дано в км/ч), переведите в км/ч умножением на 3,6, а затем из полученного числа вычтите 40 км/ч. Должны получить примерно 102 км/ч.
Почему сила трения сонаправлена со скоростью и ускорением? Разве она не должна быть против движения?
Потому что это сила трения покоя между колесами автомобиля и землей, а не сила трения скольжения. Следует различать эти силы между собой.
Но ведь есть сила трения качения. Разве не она здесь будет участвовать и будет направлена в противоположную сторону к ускорению?
Если быть точным, то момент силы трения качения, а не сила трения качения, он (момент) действует на колесо. В данном случае этим моментом следует пренебречь.
Несовсем понял как вы приравняли 3 и 4 формулы
Upd : а нет, все спасибо, разобрался

Прост надо было тщательнее перечитать то, что вы написали
Почему ma=Fтр.п.??
Задайтесь таки вопросом: какая сила заставляет двигаться автомобиль равноускоренно? Ответ на этот вопрос — сила трения покоя между колесами автомобиля и мостом.
А что если будет не сила трения покоя а сила трения скольжения?
Колеса будут проскальзывать. В этом случае вообще возможно, что автомобиль будет стоять на месте.