Условие задачи:
Луч света падает на систему двух взаимно перпендикулярных зеркал. Угол падения на первое зеркало \(\alpha = 17^\circ\). Отражаясь от первого зеркала, луч падает на второе. Определите угол отражения луча от второго зеркала.
Задача №10.1.5 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha = 17^\circ\), \(\gamma — ?\)
Решение задачи:
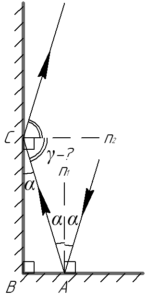 Чтобы решить эту задачу, разумеется, нужно нарисовать рисунок. Луч света, падая на нижнее зеркало под углом \(\alpha\) к нормали n1, согласно закону отражения света отразится от него под этим же углом \(\alpha\) и продолжит своё движение к другому зеркалу. Луч достигнет другое зеркало в точке C (смотрите рисунок). Так как зеркала установлены перпендикулярно друг другу, то второе зеркало параллельно нормали n1 первого зеркала. Это значит, что угол ACB и угол отражения от нижнего зеркала равны друг другу как накрест лежащие (на рисунке я уже учел этот факт и обозначил угол ACB как угол \(\alpha\)). Понятно, что луч от второго зеркала также отразится с выполнением закона отражения света, причем на рисунке прекрасно видно, что угол \(\alpha\) и искомый угол \(\gamma\) дополняют друг друга до прямого угла, поэтому:
Чтобы решить эту задачу, разумеется, нужно нарисовать рисунок. Луч света, падая на нижнее зеркало под углом \(\alpha\) к нормали n1, согласно закону отражения света отразится от него под этим же углом \(\alpha\) и продолжит своё движение к другому зеркалу. Луч достигнет другое зеркало в точке C (смотрите рисунок). Так как зеркала установлены перпендикулярно друг другу, то второе зеркало параллельно нормали n1 первого зеркала. Это значит, что угол ACB и угол отражения от нижнего зеркала равны друг другу как накрест лежащие (на рисунке я уже учел этот факт и обозначил угол ACB как угол \(\alpha\)). Понятно, что луч от второго зеркала также отразится с выполнением закона отражения света, причем на рисунке прекрасно видно, что угол \(\alpha\) и искомый угол \(\gamma\) дополняют друг друга до прямого угла, поэтому:
\[\alpha + \gamma = 90^\circ \]
Откуда:
\[\gamma = 90^\circ — \alpha \]
Посчитаем численного значение искомого угла:
\[\gamma = 90^\circ — 17^\circ = 73^\circ \]
Ответ: 73°.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
10.1.4 От подъемного крана, освещенного солнцем, падает тень длиной 75 м, а тень от вертикально
10.1.6 Над центром круглого бассейна радиусом 5 м, залитого до краев водой, висит лампа
10.1.7 Высота Солнца над горизонтом 38°. Под каким углом к горизонту надо расположить