Как известно, при равноускоренном движении зависимости скорости \(\overrightarrow \upsilon\) и перемещения \(\overrightarrow S\) тела от времени задаются формулами
\[\overrightarrow \upsilon = \overrightarrow {{\upsilon _0}} + \overrightarrow a t\;\;\;\;(1)\]
\[\overrightarrow S = \overrightarrow {{\upsilon _0}} t + \frac{{\overrightarrow a {t^2}}}{2}\;\;\;\;(2)\]
где начальная скорость \(\overrightarrow {{\upsilon _0}}\) и ускорение тела \(\overrightarrow a\) — не зависящие от времени векторы.
Упражнение 1. Из формул (1) и (2) получите следующие выражения:
\[\overrightarrow S = \frac{{\overrightarrow {{\upsilon _0}} + \overrightarrow \upsilon }}{2}t\]
\[{\upsilon ^2} — \upsilon _0^2 = 2\overrightarrow a \cdot \overrightarrow S\;\;\;\;(3)\]
Упражнение 2. Убедитесь, что из формулы (2) после дифференцирования по времени получается выражение (1).
Среди всевозможных случаев равноускоренного движения особое место занимает свободное падение тел в поле тяжести. Решение большинства задач на эту тему сводится, как правило, к применению формул (1), (2) и (3). На этом примере мы и рассмотрим основные методы работы с векторными уравнениями.
Задача 1
Тело, брошенное с поверхности земли под углом \(\alpha\) к горизонту, упало на расстоянии \(L\) от места броска. Определите время полета тела.
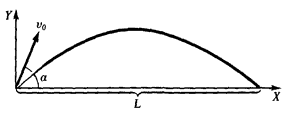
Решение 1. Выберем оси координат \(X\) и \(Y\) так, как показано на рисунке 1, и запишем векторное уравнение (2) в проекциях на эти оси:
\[\begin{gathered}
x = {\upsilon _0}\cos \alpha \cdot t \;\;\;\;(4)\hfill \\
y = {\upsilon _0}\sin \alpha \cdot t — \frac{{g{t^2}}}{2} \hfill \\
\end{gathered} \]
Пусть \(\tau\) — искомое время полета. Из условия задачи следует, что при \(t = \tau\) тело имеет координаты \(X = L\) и \(Y = 0\). Уравнения (4), записанные для момента падения тела, дают систему из двух уравнений с двумя неизвестными
\[\begin{gathered}
L = {\upsilon _0}\cos \alpha \cdot \tau \;\;\;\;(5)\hfill \\
0 = {\upsilon _0}\sin \alpha \cdot \tau — \frac{{g{\tau ^2}}}{2} \hfill \\
\end{gathered} \]
Отсюда, исключив \(\upsilon_0\), находим
\[\tau = \sqrt {\frac{{2L{\text{tg}}\alpha }}{g}} \]
Мы решили задачу стандартным методом, который можно назвать «проектированием на оси». С его помощью векторное уравнение сводится к системе скалярных, которая затем решается обычным образом. Именно так абитуриенты обычно и решают подобные задачи, однако при ответе даже несложные вопросы зачастую ставят их в тупик. Например, такие:
1) Какая разница между системами уравнений (4) и (5)?
2) Почему из трех уравнений (1) — (3), описывающих равноускоренное движение, для проектирования выбрано второе?
3) Почему именно так направлены оси координат?
Упражнение 3. Прежде чем читать ответы, подумайте, как бы вы ответили на эти вопросы.
Вы, конечно же, решали задачи с числовыми данными и знаете, что обычно требуется сначала получить буквенный ответ, или, как принято говорить, ответ в общем виде, а потом подставить в него числа. Понятно, что в буквенном ответе содержится несоизмеримо больше информации, чем в числовом. Так вот, система (4) находится примерно в таком же отношении к системе (5), как и буквенный ответ к числовому. Так, если первая система верна всегда, т. е. из нее можно найти координаты тела в любой момент времени, то вторая верна только для момента падения тела.
По поводу второго вопроса заметим, что три изменяющиеся со временем величины \(\overrightarrow \upsilon\), \(\overrightarrow S\) и \(t\) в уравнения (1) — (3) входят парами. В нашей задаче известна дальность \(\left( {\overrightarrow S } \right)\), а найти нужно время \(\left( t \right)\), поэтому мы и выбрали уравнение с парой \(\overrightarrow S\), \(t\), т. е. второе.
Упражнение 4. Как нужно переделать условие задачи, чтобы она решалась с помощью уравнений (1) или (3)?
Заметим, что эти соображения легко переносятся на задачи из любого раздела физики. Ведь все встречающиеся в задаче величины можно разбить на три группы: известные величины; неизвестные величины, которые необходимо найти; неизвестные величины, которые не требуется находить. Ясно, что если в формулы не входят первые два типа, то задачу не решить, а вот от третьих желательно по возможности избавиться.
Что касается третьего вопроса, то вы, наверное, посчитаете его глупым и скажете, что, конечно же, именно эти оси координат самые удобные. Вообще в такой задаче мысль направить оси куда-нибудь еще выглядит крамольной. И это легко обосновать. Действительно, естественно считать метод удобнее, если он позволяет получить ответ при меньшем количестве вычислений. В этом смысле наибольшие неприятности в уравнении (2) сулит член \(\frac{{\overrightarrow g {t^2}}}{2}\) — из-за него уравнения получаются квадратными. Если мы не хотим решать два квадратных уравнения, одну ось нужно направить горизонтально. Вторую же можно направить куда угодно, но, чтобы не вводить при проектировании новых углов, направим ее вертикально. Кроме того, дальность полета и высота, обычно фигурирующие в подобных задачах, являются координатами именно при таком выборе осей. Убедительно, не правда ли? И все-таки…
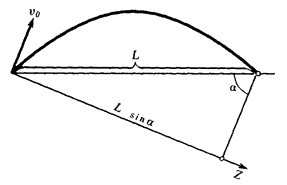
Решение 2. Направим ось \(Z\) перпендикулярно начальной скорости \(\overrightarrow {{\upsilon _0}}\) (рис. 2). В проекциях на эту ось вместо уравнения (2) получим
\[z = \frac{{g\cos \alpha \cdot {t^2}}}{2}\]
При \(t = \tau\) \(z = L\sin \alpha\). Отсюда получаем ответ:
\[\tau = \sqrt {\frac{{2L{\text{tg}}\alpha }}{g}} \]
Это решение стало возможным потому, что величина третьего типа (по нашей классификации) \(\overrightarrow {{\upsilon _0}}\) — векторная, и от нее можно избавиться удачным выбором оси координат, получив тем самым одно уравнение с одним неизвестным.
Впрочем, можно вообще обойтись без всяких осей…
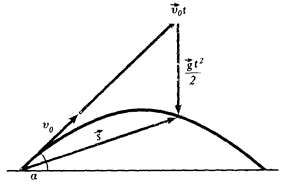
Решение 3. Формула (2) утверждает, что при равноускоренном движении вектор перемещения тела в любой момент времени равен сумме векторов \(\overrightarrow {{\upsilon _0}} t\) и \(\frac{{\overrightarrow g {t^2}}}{2}\) (рис. 3). Это, кстати, означает, что движение тела, брошенного под углом к горизонту, складывается из равномерного и прямолинейного движения со скоростью \(\overrightarrow {{\upsilon _0}}\) и свободного падения без начальной скорости.
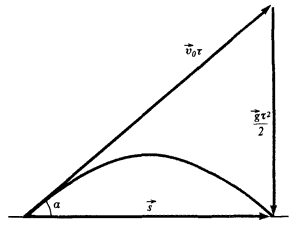
«Нарисуем» формулу (2) для момента падения тела \(\tau\) (рис. 4). Из получившегося прямоугольного треугольника легко найдем
\[L{\text{tg}}\alpha = \frac{{g{\tau ^2}}}{2}{\text{,}}\,\,{\text{}}\,\,\tau = \sqrt {\frac{{2L{\text{tg}}\alpha }}{g}} \]
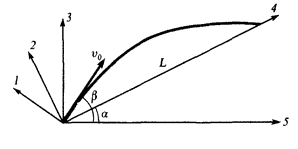
Упражнение 5. Тело бросают под углом \(\beta\) к горизонту со склона горы, наклоненной под углом \(\alpha\) к горизонту. Тело упало на расстоянии \(L\) от места броска. 1) Напишите уравнения движения тела (уравнение (2)) в проекциях на оси 1—5 (рис. 5) для момента падения тела на склон горы. 2) Выберете любые два из этих уравнений и покажите, что оставшиеся можно получить из этих двух. 3) Для каждого из полученных уравнений придумайте задачу, в которой это уравнение сразу приводит к цели.
Задача 2
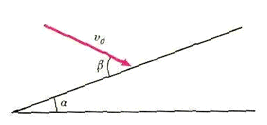
На гладкую неподвижную наклонную плоскость с углом наклона \(\alpha\) налетает стальной шарик под углом \(\beta\) к плоскости (рис. 6). При каких значениях \(\beta\) шарик сможет вернуться в точку его первого удара о плоскость? Все соударения считать упругими.
Ограничимся одним — наиболее разумным, с нашей точки зрения, решением этой задачи.
Решение. Движение шарика в целом в этом случае не является равноускоренным из-за ударов о плоскость. Однако в промежутках между ударами шарик движется под действием только силы тяжести и, следовательно, равноускоренно. Поэтому для каждого промежутка можно использовать формулы (1) — (3), правда для этого всякий раз нам придется искать начальную скорость.
Как известно, при упругом ударе составляющая скорости шарика, параллельная плоскости, не изменяется, а перпендикулярная плоскости составляющая лишь меняет знак, также не изменяясь по величине. Тогда, зная скорость шарика \(\overrightarrow {{\upsilon _0}}\) перед первым ударом, найдем скорость после этого удара и подставим ее в формулу (2) для первого участка равноускоренного движения. Затем по формуле (1) найдем скорость шарика перед вторым ударом, и т. д. Другими словами, формулы (1) — (3) плюс условия упругого удара полностью определяют движение шарика.
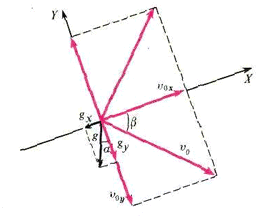
Осталось только определиться с выбором осей. Если, по традиции, направить оси горизонтально и вертикально, то мы, конечно, выиграем при написании уравнений движения для отдельных участков (так как проекция шарика на горизонтальную ось движется равномерно), но зато очень сложными станут условия отскока шарика. Поэтому направим оси \(X\) и \(Y\) так, как показано на рисунке 7, и запишем уравнение (2) в проекциях на эти оси:
\[x = {\upsilon _{0x}}t + \frac{{{g_x}{t^2}}}{2},\]
\[y = {\upsilon _{0y}}t + \frac{{{g_y}{t^2}}}{2},\]
где
\[{\upsilon _{0x}} = {\upsilon _0}\cos \beta ,\,\,\,{\upsilon _{0y}} = {\upsilon _0}\sin \beta ,\]
\[{g_x} = — g\sin \alpha ,\,\,\,{g_y} = — g\cos \alpha .\]
Шарик ударится о плоскость второй раз, когда координата \(y\) станет равна нулю (еще одно преимущество выбранных нами осей). Решив уравнение
\[0 = {\upsilon _{0y}}\tau + \frac{{{g_y}{\tau ^2}}}{2},\]
найдем, что второй удар произойдет через время
\[\tau = \frac{{2{\upsilon _{0y}}}}{{ — {g_y}}} = \frac{{2{\upsilon _0}\sin \beta }}{{g\cos \alpha }}.\]
Чтобы найти скорость шарика перед вторым ударом (т. е. через время \(\tau\)), запишем в проекциях на наши оси уравнение (1):
\[{\upsilon _x} = {\upsilon _{0x}} + {g_x}t,\]
\[{\upsilon _y} = {\upsilon _{0y}} + {g_y}t.\]
Подставляя \(t = \tau = \frac{{2{\upsilon _{0y}}}}{{ — {g_y}}}\), получим, что перед вторым ударом \({\upsilon _y} = — {\upsilon _{0y}}\) и, следовательно, сразу после удара \({\upsilon _y} = {\upsilon _{0y}}\). Этот результат позволяет облегченно вздохнуть — дальше можно не считать. Так как время между ударами зависит только от \({\upsilon _{0y}}\), все удары происходят через одинаковое время.
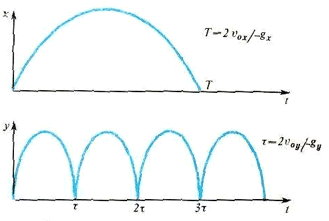
Ответить на вопрос задачи теперь удобнее всего, нарисовав друг под другом графики зависимости координат шарика от времени (рис. 8). Шарик вернется в ту же точку, если в некоторый момент \(x = y = 0\), что может быть, только если \(T = n\tau\), где \(n\) — целое число. Итак,
\[\frac{{2{\upsilon _0}\cos \beta }}{{g\sin \alpha }} = n\frac{{2{\upsilon _0}\sin \beta }}{{g\cos \alpha }},\]
откуда
\[{\text{ctg}}\beta = n{\text{tg}}\alpha .\]
Интересно, что при четных и нечетных \(n\) шарик ведет себя несколько по-разному. При четных \(n\) средний удар шарика (всего ударов \(n + 1\)) происходит перпендикулярно плоскости, и шарик возвращается обратно по той же траектории. Если же \(n\) нечетно, то после половины ударов шарик летит вертикально вверх, падает обратно и также возвращается, повторяя весь пройденный путь.
Задача 3
В область пространства, где создано горизонтальное электрическое поле с напряженностью \(\overrightarrow E\), запускают шарик, масса которого \(m\), а заряд \(q\), со скоростью \(\overrightarrow {{\upsilon _0}}\), направленной вертикально вверх. Какова минимальная скорость шарика в процессе движения?
Вас не удивило присутствие здесь «электрической» задачи? Нет? И правильно, эта задача, конечно же, имеет прямое отношение к кинематике.
Обсудим два решения.
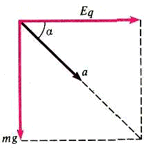
Решение 1. На шарик в полете действуют две постоянные силы: сила тяжести \(m\overrightarrow g\) и электрическая сила \(\overrightarrow E q\) (рис. 9). По второму закону Ньютона ускорение шарика постоянно и равно
\[\overrightarrow a = \frac{{\overrightarrow E q + m\overrightarrow g }}{m}.\]
При этом
\[a = \left| {\overrightarrow a } \right| = \frac{{\sqrt {{{\left( {Eq} \right)}^2} + {{\left( {mg} \right)}^2}} }}{m}.\]
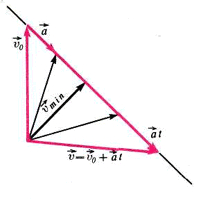
На рисунке 10 показано, как изменяется со временем вектор скорости шарика («нарисована» формула (1)). Ясно, что минимальной скорость будет через время
\[t = \frac{{{\upsilon _0}\sin \alpha }}{a}\]
и ее величина будет равна
\[{\upsilon _{\min }} = {\upsilon _0}\cos \alpha = {\upsilon _0}\frac{{Eq}}{{\sqrt {{{\left( {Eq} \right)}^2} + {{\left( {mg} \right)}^2}} }}\]
Если вам хочется побольше формул, можно сделать по-другому.
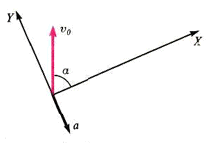
Решение 2. Направим оси координат перпендикулярно и параллельно ускорению (рис. 11) и запишем уравнение (1) в проекциях на эти оси:
\[{\upsilon _x} = {\upsilon _0}\cos \alpha ,\]
\[{\upsilon _y} = {\upsilon _0}\sin \alpha — at.\]
(Сравните co свободным падением тела, брошенного под углом к горизонту.) Так как оси перпендикулярны,
\[\upsilon = \sqrt {\upsilon _x^2 + \upsilon _y^2} = \sqrt {{{\left( {{\upsilon _0}\cos \alpha } \right)}^2} + {{\left( {{\upsilon _0}\sin \alpha — at} \right)}^2}} .\]
Так как \({\left( {{\upsilon _0}\sin \alpha — at} \right)^2} \geq 0\),
\[\upsilon \geq {\upsilon _0}\cos \alpha ,\]
и при \(t = \frac{{{\upsilon _0}\sin \alpha }}{a}\)
\[{\upsilon _{\min }} = {\upsilon _0}\cos \alpha .\]
Подставляя сюда выражение для \(\cos \alpha\), получим прежний ответ.
Если вы располагаете большим количеством свободного времени и чистой бумаги, убедитесь, что при другом выборе осей решение, мягко говоря, проще не становится.
Задачи для самостоятельной работы
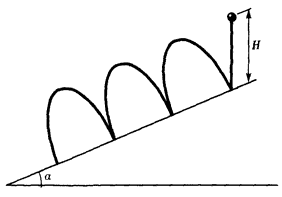
- Шарик свободно падает с высоты \(H\) на наклонную плоскость, составляющую угол \(\alpha\) с горизонтом (рис. 12). Найдите отношение расстояний между точками, в которых подпрыгивающий шарик касается наклонной плоскости. Соударения шарика с плоскостью считать абсолютно упругими.
- Из миномета ведут стрельбу по объектам, расположенным на склоне горы. На каком расстоянии от миномета будут падать мины, если время их полета \(\tau\)? Угол наклона горы к горизонту \(\beta\), миномет стреляет под углом \(\alpha\) к горизонту.
- Со стола высотой \(H\) сбрасывают упругий шарик, сообщая ему некоторую горизонтальную скорость. В момент, когда шарик испытывает одно из бесчисленных упругих соударений с полом, с того же стола горизонтально сбрасывают другой шарик, сообщая ему такую скорость, чтобы он столкнулся с первым шариком. На какой высоте произойдет встреча?
- Электрон влетает в плоский конденсатор, параллельно его пластинам, со скоростью \({\upsilon _0} = 2 \cdot {10^6}\) м/с. Найдите модуль скорости электрона в момент его вылета из конденсатора. Напряженность поля в конденсаторе \(E = 100\) В/м, длина пластин \(L = 8\) см, заряд электрона \(e = 1,6 \cdot {10^{ — 19}}\) Кл, его масса \(m = 9,1 \cdot {10^{ — 34}}\) кг.
Источник: Журнал “Квант”, №2 1991 г. Автор: Д. Александров.