Явление преломления света на сферической поверхности раздела двух оптических сред позволяет получать изображения светящихся предметов. Эта возможность осуществляется с помощью линзы — прозрачного тела, ограниченного двумя сферическими поверхностями. Линза является основным оптическим элементом в таких приборах, как фотоаппарат, проекционный фонарь, микроскоп, телескоп и т. д.
На рисунке 1 показан разрез преломляющей сферической поверхности, разделяющей две оптические среды с различными показателями преломления. Очевидно, качественное изображение любого предмета возможно только в том случае, когда пучок лучей, исходящих из любой точки предмета (например, из точки \(P\)), после преломления соберется снова в точку. Вообще говоря, сферическая граница раздела двух сред не обеспечивает этого условия. Так, луч \(NB\) после преломления пересечет ось \(PQ\), строго говоря, в другой точке, нежели луч \(MA\). Однако при некоторых условиях пучок лучей, испущенных точкой, может собраться практически в точку. Это будет в том случае, когда высота \(h\), на которой все лучи этого пучка пересекают преломляющую поверхность, мала по сравнению с радиусом кривизны \(OC\) преломляющей поверхности. Другими словами, когда мал угол \(\alpha\). Лучи, удовлетворяющие этому условию, называются параксиальными. Для удаленных источников требование малости угла \(\alpha\) эквивалентно требованию малости угла \(u\). Но малость угла \(u\) не является достаточным условием параксиальности. Действительно, луч, параллельный оси \(PQ\) (\(u = 0\)), но достаточно удаленный от нее (\(h\) велико), не будет параксиальным.
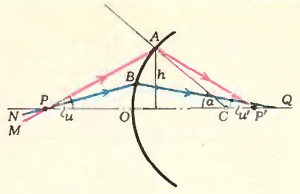
Таким образом, в зависимости от того, сколь хорошо выполняется условие параксиальности, в окрестности точки \(P\) будет более или менее большой кружок размытия. Однако на практике нет необходимости делать его меньше некоторой, вполне определенной, величины. Например, если кружок размытия станет меньше элемента сетчатки глаза (зерна фотоэмульсии на фотопленке, неровностей матового стекла и т. п.), он будет восприниматься нами как точка. Его дальнейшее уменьшение в нашем зрительном ощущении ничего не изменит.
Всюду в дальнейшем мы будем иметь дело только с параксиальными лучами (можно, в принципе, придумать такие преломляющие поверхности, для которых условие параксиальности лучей не является обязательным. Однако наиболее просты в изготовлении именно сферические поверхности). Кроме того, ограничимся рассмотрением только тонких линз, то есть таких линз, фокусные расстояния которых существенно больше их толщины.
Если тонкая линза изготовлена из материала с показателем преломления \(n\), слева от линзы находится среда показателем преломления \(n_1\), а справа — с показателем преломления \(n_2\), то имеют место соотношения:
\(\frac{{{n_2}}}{{{F_2}}} = \frac{{n — {n_1}}}{{{R_1}}} + \frac{{n — {n_2}}}{{{R_2}}}\), (1)
\(\frac{{{n_1}}}{{{F_1}}} = \frac{{n — {n_1}}}{{{R_1}}} + \frac{{n — {n_2}}}{{{R_2}}}\), (2)
Здесь \(F_1\) и \(F_2\) — переднее и заднее фокусные расстояния линзы, \(R_1\) и \(R_2\) — радиусы кривизны, соответственно, передней и задней поверхностей линзы. Эти соотношения можно получить (проделайте это самостоятельно!), рассматривая ход лучей, идущих от бесконечно удаленного источника, находящегося в первом случае слева от линзы, а втором случае — справа. В частности, когда с обеих сторон от линзы находится воздух (\(n_1 = n_2 = 1\)),
\(\frac{1}{{{F_1}}} = \frac{1}{{{F_2}}} = \left( {n — 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\). (3)
Принято считать, что если поверхность своей выпуклой стороной обращена к среде с меньшим показателем преломления, то ее радиус кривизны \(R\) положителен (\(R > 0\)), в противном случае \(R < 0\). Линзы, у которых фокусное расстояние положительно (\(F > 0\)), называются положительными или собирающими, если же \(F < 0\) — отрицательными или рассеивающими. Величина \(D = \frac{1}{F}\) называется оптической силой линзы; она измеряется в диоптриях.
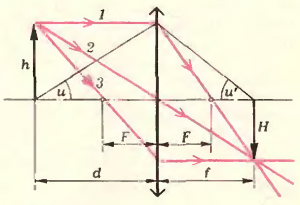
При построении изображений, полученных с помощью тонких линз, используют три основных (или базисных) луча, показанных на рисунке 2. С помощью этого рисунка нетрудно получить формулу тонкой линзы:
\(\frac{1}{d} + \frac{1}{f} = \frac{1}{F}\),
а также выражения для её линейного (поперечного) увеличения:
\(\Gamma = \frac{H}{h} = \frac{f}{d} = \frac{{f — F}}{F} = \frac{F}{{d — F}}\)
и для углового увеличения:
\(\gamma = \frac{{tg\,u’}}{{tg\,u}} = \frac{{h/f}}{{h/d}} = \frac{d}{f} = \frac{1}{\Gamma }\).
Рассмотрим теперь несколько конкретных задач.
Задача 1
На поверхности воды \(n_в = 1,3\) лежит двояковыпуклая тонкая стеклянная линза \(n_{ст} = 1,5\) с радиусами кривизны \(R_1 = R_2 = 10\) см. Определите переднее и заднее фокусные расстояния линзы. Чему равно фокусное расстояние этой линзы в воздухе?
Это относительно простая задача. Непосредственное применение формул (1) и (2), где \(n_1 = 1\), \(n_2 = n_в = 1,3\) и \(n = n_{ст} = 1,5\), дает
\({F_1} \approx 14\) см и \({F_2} \approx 18,5\) см.
Для фокусного расстояния линзы в воздухе формула (3) приводит к результату \(F = 10\) см.
Задача 2
На рисунке 3 дан ход луча \(ABC\) через тонкую положительную линзу. Построить ход произвольного луча \(DE\) после преломления в линзе.
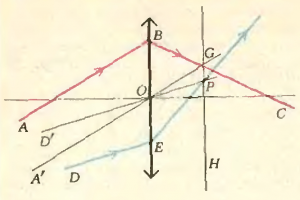
Проведем \(A’O\), параллельный лучу \(AB\) и проходящий через оптический центр линзы. Он не преломится. Точка \(O\) пересечения этого луча с лучом \(BC\) лежит в фокальной плоскости \(H\). Луч \(D’O\), параллельный \(DE\), пересечет фокальную плоскость в точке \(P\). Через эту же точку пройдет, преломившись, и луч \(DE\).
3адача 3
Какие очки вы пропишите близорукому человеку, который может читать текст, расположенный не далее 20 см?
Очки ни в коей мере не исправляют дефектов человеческого глаза. Их роль сводится к тому, чтобы отобразить объекты окружающего мира на такое расстояние, с которого глаз четко различает предметы. В нашем случае для того чтобы близорукий человек мог видеть удаленные предметы, например, звезду, очки должны создавать изображение звезды не далее 20 см от глаза, а глаз будет рассматривать уже это изображение. Предположим, что линза очков вплотную придвинута к глазу (небольшой зазор между линзой и глазом несущественно исказит приведенные ниже расчеты), и запишем формулу линзы:
\(\frac{1}{d} — \frac{1}{f} = \frac{1}{F}\),
Здесь \(d\) —расстояние до звезды, а \(f\) — максимальное расстояние от изображения звезды до глаза. Член \(\frac{1}{f}\) берется со знаком минус, поскольку изображение мнимое. Так как \(d\) очень велико, можно смело положить \(\frac{1}{d} = 0\). По условию задачи \(f = 20\) см. Отсюда
\(F = — 20\) см, \(D = — 5\) дптр.
Таким образом, близорукому человеку следует прописать очки с рассеивающими линзами оптической силы -5 дптр.
Задача 4
С помощью линзы с фокусным расстоянием \(F\) на экране получают уменьшенное и увеличенное изображения предмета, находящегося на расстоянии \(L\) от экрана. Найти отношение размеров изображений.
Пусть высота предмета равна \(h\). Тогда изображение имеет высоту \(H = \Gamma h\), и отношение размеров изображений есть
\(\frac{{{H_1}}}{{{H_2}}} = \frac{{{\Gamma _1}h}}{{{\Gamma _2}h}} = \frac{{{f_1}/{d_1}}}{{{f_2}/{d_2}}}\).
Теперь нам нужно найти \(d_1\), \(d_2\), \(f_1\) и \(f_2\). По формуле линзы \(\frac{1}{d} + \frac{1}{f} = \frac{1}{F}\), а из условия задачи \(d + f = L\). Исключив \(d\), получим квадратное уравнение
\[{f^2} — fL + FL = 0,\]
откуда
\[{f_{1,2}} = \frac{L}{2} \pm \sqrt {\frac{{{L^2}}}{4} — FL} .\]
Кроме того, из свойства обратимости лучей \(d_1 = f_2\) и \(d_2 = f_1\). Таким образом,
\[\frac{{{H_1}}}{{{H_2}}} = \frac{{f_1^2}}{{f_2^2}} = {\left( {\frac{{L/2 + \sqrt {{L^2}/4 — FL} }}{{L/2 — \sqrt {{L^2}/4 — FL} }}} \right)^2}.\]
Задача 5
С помощью положительной линзы получают изображения двух точечных источников \(A\) и \(B\). Один из них расположен на оптической оси на двойном фокусном расстоянии от линзы, другой смещен от оси так, что прямая, соединяющая источники, образует с оптической осью угол \(\varphi = 30^\circ\) (рис. 4) Под каким углом \(\psi \) к оси следит расположить плоский экран, чтобы одновременно получить на нем четкие изображения обоих источников?
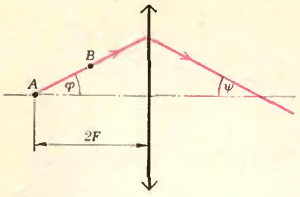
Очевидно, экран нужно расположить по лучу \(AB\) (проведенному от источника \(A\) через точку \(B\)) после его преломления в линзе. Используем формулу для углового увеличения:
\(\gamma = \frac{1}{\Gamma } = \frac{d}{f} = \frac{F}{f-F}\).
Здесь \(f\) — расстояние от изображения источника \(A\) до линзы, a \(F\) — фокусное расстояние линзы. Поскольку \(A\) находится на двойном фокусном расстоянии от линзы, \(f = 2F\). Следовательно,
\(\gamma = \frac{F}{{2F — F}} = 1,\) и \(\psi = \varphi = 30^\circ \).
Задача 6
Сложный объектив состоит из двух тонких линз: положительной с фокусным расстоянием \(F_1 = 20\) см и отрицательной с фокусным расстоянием \(F_2 = -10\) см. Линзы расположены на расстоянии \(l = 15\) см друг от друга. С помощью объектива получают на экране изображение Солнца. Какое фокусное расстояние \(f\) должна иметь тонкая линза, чтобы изображение Солнца, полученное с ее помощью, имело такой же размер?
Здесь мы уже имеем дело с системой линз.
Найдем размер изображения Солнца, создаваемого сложным объективом, рассматривая ход лучей последовательно в обеих линзах. Изображение, создаваемое первой линзой, находится, очевидно, в ее фокальной плоскости. Размер этого изображения \({H_1} = {F_1}tg\alpha \), где \(\alpha\) — угловой диаметр Солнца, видимый с Земли (рис.5). Увеличение, даваемое второй линзой, равно \(\frac{{{H_2}}}{{{H_1}}} = \frac{{{f_2}}}{{{d_2}}}\). По формуле линзы имеем
\[ — \frac{1}{{{d_2}}} + \frac{1}{{{f_2}}} = \frac{1}{{{F_2}}},\]
где \(d_2 = F_1 — l\) (изображение Солнца в первой линзе является мнимым источником для второй). Отсюда
\[{f_2} = \frac{{{F_2}\left( {{F_1} — l} \right)}}{{{F_1} + {F_2} — l}}.\]

Таким образом, размер изображения, создаваемого всем объективом,
\[{H_2} = \frac{{{F_1}{F_2}tg\alpha }}{{{F_1} + {F_2} — l}}.\]
Одиночная линза с фокусным расстоянием \(F\) дает изображение, имеющее размер \({H_2} = F\;tg\alpha \). Сопоставляя два последних выражения, получим
\[F = \frac{{{F_1}{F_2}}}{{{F_1} + {F_2} — l}} = \frac{{20\left( { — 10} \right)}}{{20 + \left( { — 10} \right) — 15}} = 40\;см\]
Только что разобранная задача является частным случаем более общей, практически важной задачи: дана система двух (или более) тонких линз с общей оптической осью; необходимо найти одну тонкую линзу, действие которой эквивалентно действию данной системы. Эта задача будет полностью решена, если мы найдем фокусное расстояние эквивалентной линзы и ее местоположение (или, что то же самое, положение ее фокуса). Попробуйте вывести соответствующие формулы самостоятельно. Для ориентировки приведем окончательные результаты: фокусное расстояние искомой эквивалентной линзы равно
\[F = \frac{{{F_1}{F_2}}}{\Delta },\]
а ее фокус находится от второй линзы на расстоянии \(f_2\), равном
\[{f_2} = \frac{{{F_2}\left( {\Delta — {F_2}} \right)}}{\Delta }.\]
Здесь \(F_1\) и \(F_2\) — фокусные расстояния первой и второй линз соответственно, а \(\Delta\) — расстояние между задним фокусом первой линзы и передним фокусом второй (его называют оптическим интервалом). Принято считать \(\Delta > 0\), если передний фокус второй линзы лежит левее заднего фокуса первой линзы, и \(\Delta < 0\) в противном случае.
В заключение предлагаем несколько задач для самостоятельного решения.
Упражнения
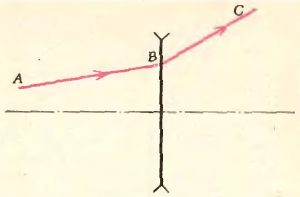
- На рисунке 6 дан ход луча \(ABC\) через тонкую отрицательную линзу. Определить построением фокусное расстояние линзы.
- Какие очки вы пропишите дальнозоркому человеку, который резко видит предметы, расположенные не ближе 50 см?
- Положительная линза дает действительное изображение с увеличением в 2 раза. Определить фокусное расстояние линзы, если расстояние между линзой и изображением 24 см.
- Предмет в виде отрезка длиной \(l\) расположен вдоль оптической оси тонкой положительной линзы с фокусным расстоянием \(F\). Середина отрезка находится на расстоянии \(d\) от линзы. Линза дает действительное изображение всех точек предмета. Определить продольное увеличение предмета.
- Положительная линза с фокусным расстоянием \(F\) и отрицательная с фокусным расстоянием \(-F\) расположены на расстоянии \(a\) друг от друга так, что их оптические оси совпадают. На расстоянии \(a\) перед положительной линзой находится источник света. Изображение этого источника, даваемое системой линз, располагается на таком же расстоянии \(a\) за отрицательной линзой. Определить это расстояние.
- Оптическая система состоит на двух линз: собирающей с фокусным расстоянием \(F_1 = 30\) см и рассеивающей с фокусным расстоянием \(F_2 = — 30\) см. Оптические оси линз совпадают. Параллельный пучок лучей падает на первую линзу и, пройдя через систему, собирается в некоторой точке, лежащей на оптической оси. На сколько сместится эта точка, если линзы поменять местами?
- В проекционном аппарате используется сложный объектив, состоящий из двух собирающих линз с фокусными расстояниями \(F_1 = 20\) см и \(F_2 = 15\) см. Линзы расположены на расстоянии \(a=5\) см друг от друга. Определить, с каким увеличением будет проецироваться диапозитив на экран, находящийся на расстоянии \(b=10\) м от объектива проектора. К диапозитиву обращена линза с фокусным расстоянием \(F_2\).
Источник: Журнал «Квант», №4 1977 г. Автор: Е. Кузнецов.