Движение тел по криволинейным траекториям часто встречается в природе и технике. Это, например, движение спутников и метеоритов в поле тяжести Земли или планет и комет в поле тяжести Солнца, движение заряженных частиц в ускорителях или деталей различных механизмов.
Напомним основные закономерности, справедливые для криволинейного движения. Как известно, скорость тела всегда направлена по касательной к его траектории и при движении может изменяться и по модулю, и по направлению. Вектор ускорения тела не совпадает по направлению со скоростью,а составляет с ней некоторый угол. Часто бывает удобнее говорить не о самом ускорении, а о двух его проекциях. Одна из них, так называемая тангенциальная (или касательная) проекция \(a_{т}\) — это проекция на направление скорости (то есть на направление касательной к траектории). Эта проекция характеризует изменение модуля скорости. Другая, так называемая нормальная (или центростремительная) проекция \(a_{н}\) — это проекция на направление, перпендикулярное к вектору скорости. Она характеризует изменение направления скорости. В частности, при равномерном движении тела по окружности ускорение имеет лишь одну проекцию — нормальную к скорости и изменяющую лишь ее направление. Модуль этой проекции равен квадрату модуля скорости, деленному на радиус окружности: \({a_н} = \frac{{{\upsilon ^2}}}{R}\).
Небольшой участок любой криволинейной траектории всегда можно представить как часть некоторой окружности; радиус соответствующей окружности называют радиусом кривизны траектории в данном месте. Поэтому выражение \({a_н} = \frac{{{\upsilon ^2}}}{R}\) можно использовать для определения радиуса кривизны траектории \(R\).
Наконец, для тела, движущегося по криволинейной траектории, так же как и для тела, движущегося прямолинейно, справедлив второй закон Ньютона: векторная сумма всех действующих на тело сил равна массе тела, умноженной на вектор его ускорения.
Рассмотрим несколько конкретных задач на криволинейное движение тел.
Задача 1
С поверхности земли брошено тело с начальной скоростью \(\overrightarrow {{\upsilon _0}}\) под углом \({\alpha _0}\) к горизонту. Найдите зависимость тангенциальной и нормальной проекций ускорения тела от его высоты подъема. Сопротивление воздуха можно не учитывать.
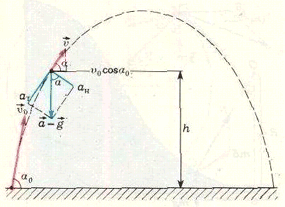
После броска на тело действует только одна сила — сила притяжения к Земле, поэтому в любой точке траектории ускорение \(\overrightarrow a\) тела равно ускорению свободного падения \(\overrightarrow g\) (рис. 1). Тангенциальная и нормальная проекции ускорения равны, соответственно,
\[{a_т} = g\sin \alpha \,\,{\text{и}}\,\,{a_н} = g\cos \alpha. \]
Здесь \(\alpha\) — угол, который составляет с горизонтом скорость \(\overrightarrow \upsilon\) тела на высоте \(h\).
Запишем закон сохранения энергии:
\[\frac{{m\upsilon _0^2}}{2} = \frac{{m{\upsilon ^2}}}{2} + mgh\]
И найдем выражение для модуля \(\upsilon\) скорости тела:
\[\upsilon = \sqrt {\upsilon _0^2 — 2gh} .\]
Во время движения проекция скорости на горизонтальное направление остается постоянной и равной \({\upsilon _0}\cos {\alpha _0}\). Тогда (см. Рис. 1)
\[{a_н} = g\cos \alpha = g\frac{{{\upsilon _0}\cos {\alpha _0}}}{\upsilon } = g\frac{{{\upsilon _0}\cos {\alpha _0}}}{{\sqrt {\upsilon _0^2 — 2gh} }}\]
и
\[{a_т} = g\sin \alpha = g\sqrt {1 — {{\cos }^2}\alpha } = g\frac{{\sqrt {\upsilon _0^2{{\sin }^2}{\alpha _0} — 2gh} }}{{\sqrt {\upsilon _0^2 — 2gh} }}.\]
В полученные формулы можно ввести максимальную высоту подъема тела \({h_{\max }} = \frac{{\upsilon _0^2{{\sin }^2}{\alpha _0}}}{{2g}}\):
\[{a_н} = g\cos {\alpha _0}\frac{{\sqrt {{h_{\max }}} }}{{\sqrt {{h_{\max }} — h{{\sin }^2}{\alpha _0}} }}\]
и
\[{a_т} = g\sin {\alpha _0}\frac{{\sqrt {{h_{\max }} — h} }}{{\sqrt {{h_{\max }} — h{{\sin }^2}{\alpha _0}} }}.\]
Задача 2
Конечный участок BC горы разгона на лыжном трамплине представляет собой дугу окружности радиусом \(R=15\) м (рис. 2). Полная высота горы \(H=50\) м. Найдите модуль ускорения лыжника в точке C, если угол \(\alpha = 15^\circ\). Считайте, что лыжник спускается с горы без начальной скорости; трением пренебрегите.
При движении по горе разгона на лыжника действуют две силы. Это — сила тяжести \(m\overrightarrow g\), направленная вертикально вниз, и сила реакции опоры \(\overrightarrow N\), направленная, в отсутствие трения, по радиусу кривизны траектории, в нашем случае — по радиусу CO. Равнодействующая этих сил и сообщает лыжнику искомое ускорение \(\overrightarrow a\):
\[m\overrightarrow a = m\overrightarrow g + \overrightarrow N .\]

По теореме косинусов для треугольника сил имеем (см. рис. 2):
\[{\left( {ma} \right)^2} = {\left( {mg} \right)^2} + {N^2} — 2mgN\cos \alpha .\]
Пусть \(\overrightarrow \upsilon\) — скорость лыжника в точке C. Нормальная проекция ускорения \({a_н} = \frac{{{\upsilon ^2}}}{R}\) создается соответствующими проекциями сил \(m\overrightarrow g\) и \(\overrightarrow N\):
\[\frac{{m{\upsilon ^2}}}{R} = N — mg\cos \alpha .\]
Исключая \(N\) из последних двух уравнений, получим:
\[{a^2} = {g^2}{\sin ^2}\alpha + {\left( {\frac{{{\upsilon ^2}}}{R}} \right)^2}.\]
Подставим сюда значение модуля v скорости лыжника из закона сохранения энергии
\[\frac{{m{\upsilon ^2}}}{2} = mg\left( {H — R\left( {1 — \cos \alpha } \right)} \right)\]
и найдем модуль ускорения лыжника:
\[a = \sqrt {{g^2}{{\sin }^2}\alpha + {{\left( {\frac{{{\upsilon ^2}}}{R}} \right)}^2}} = g\sqrt {{{\sin }^2}\alpha + 4{{\left( {\frac{H}{R} — 1 + \cos \alpha } \right)}^2}} \approx 65\;м/с^2.\]
Это же значение можно получить из несколько других рассуждений. При движении по дуге окружности нормальная проекция ускорения равна \({a_н} = \frac{{{\upsilon ^2}}}{R}\), а тангенциальная проекция, создаваемая только соответствующей проекцией силы тяжести, равна \({a_т} = g\sin \alpha\). Тогда модуль ускорения равен:
\[a = \sqrt {a_н^2 + a_т^2} = \sqrt {{g^2}{{\sin }^2}\alpha + {{\left( {\frac{{{\upsilon ^2}}}{R}} \right)}^2}} \]
Задача 3
Небольшое тело, находящееся на полусфере, начинает скользить по ней без трения (рис.3). Определите координаты точки, в которой тело достигнет горизонтальной плоскости.
Некоторое время после начала движения тело будет скользить по полусфере, а потом, оторвавшись от нее, будет двигаться как тело, брошенное под углом к горизонту.
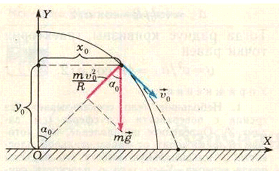
Введем систему координат XOY, как указано на рисунке 3. Сначала найдем координаты \(x_0\) и \(y_0\) точки отрыва тела от полусферы, а также модуль и направление скорости \(\overrightarrow {{\upsilon _0}}\) в момент отрыва. Движение тела по полусфере происходит под действием двух сил — силы тяжести \(m\overrightarrow g\) и силы нормальной (так как отсутствует трение) реакции \(\overrightarrow N\). В момент отрыва сила реакции обращается в нуль, так что нормальное ускорение \({a_н} = \frac{{{\upsilon ^2}}}{R}\) телу сообщается только соответствующей проекцией силы тяжести:
\[\frac{{m\upsilon _0^2}}{R} = mg\cos {\alpha _0}.\]
Решая это уравнение совместно с уравнением, выражающим закон сохранения энергии:
\[\frac{{m\upsilon _0^2}}{2} = mgR\left( {1 — \cos {\alpha _0}} \right),\]
найдем
\[\cos {\alpha _0} = \frac{2}{3},\,\,{\upsilon _0} = \sqrt {\frac{{2gR}}{3}} .\]
Координаты точки отрыва равны, соответственно,
\[{y_0} = R\cos {\alpha _0} = \frac{{2R}}{3},\]
\[{x_0} = \sqrt {{R^2} — y_0^2} = R\sqrt {1 — {{\cos }^2}{\alpha _0}} = \frac{{\sqrt 5 R}}{3}.\]
Теперь запишем уравнения движения тела после отрыва от полусферы:
\[x = {x_0} + {\upsilon _0}\cos {\alpha _0} \cdot t,\]
\[y = {y_0} — {\upsilon _0}\sin {\alpha _0} \cdot t — \frac{{g{t^2}}}{2}.\]
Очевидно, что в момент достижения горизонтальной плоскости координата \(y\) становится равной нулю: \(y=0\). Координату \(x\) найдем из соответствующего уравнения движения, подставив туда значения начальных условий (\(x_0\), \(\upsilon_0\) и \(\cos {\alpha _0}\)), а также время полета до удара, полученное из условия \(y=0\):
\[x \approx 1,12R.\]
Задача 4
По горизонтальной поверхности с постоянной скоростью \(\overrightarrow {{\upsilon _0}}\) катится без проскальзывания колесо радиусом \(R\). На ободе колеса находится материальная точка массой \(m\). Определите модуль и направление силы реакции, действующей на точку, а также радиус кривизны ее траектории в зависимости от положения точки на ободе.
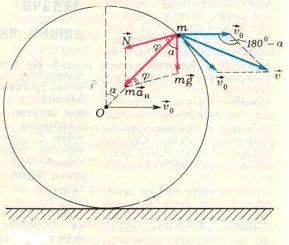
Пусть мгновенное положение материальной точки на ободе колеса характеризуется углом \(\alpha\) (рис. 4). С точки зрения наблюдателя в неподвижной системе координат (например, связанной с землей) точка участвует в двух движениях — в поступательном движении вместе с колесом с постоянной горизонтальной скоростью \(\overrightarrow {{\upsilon _0}}\) и во вращательном движении вокруг центра колеса с угловой скоростью \(\frac{{{\upsilon _0}}}{R}\).
Воспользуемся тем, что в различных инерциальных системах координат ускорения тела одинаковы. Рассмотрим систему координат, движущуюся вместе с центром колеса со скоростью \(\overrightarrow {{\upsilon _0}}\). В этой системе материальная точка равномерно движется по окружности. Нормальное ускорение \(\overrightarrow {{a_н}}\) (\({a_н} = \frac{{{\upsilon ^2}}}{R}\)) ей сообщают две силы — сила тяжести \(m\overrightarrow g\) и сила реакции \(\overrightarrow N\). По теореме косинусов из треугольника сил имеем (см. рис. 4)
\[{N^2} = {\left( {mg} \right)^2} + {\left( {\frac{{m\upsilon _0^2}}{R}} \right)^2} — 2\left( {mg} \right)\left( {\frac{{m\upsilon _0^2}}{R}} \right)\cos \alpha ,\]
откуда
\[N = \sqrt {{{\left( {mg} \right)}^2} + {{\left( {\frac{{m\upsilon _0^2}}{R}} \right)}^2} — 2\left( {mg} \right)\left( {\frac{{m\upsilon _0^2}}{R}} \right)\cos \alpha } .\]
Направление силы \(\overrightarrow N\), определяемое углом \(\varphi\), можно найти из того же треугольника по теореме синусов:
\[\frac{N}{{\sin \alpha }} = \frac{{mg}}{{\sin \varphi }},\]
\[\varphi = \arcsin \frac{{mg}}{{N\sin \alpha }}.\]
Найдем теперь радиус кривизны траектории точки. Как мы уже говорили, в неподвижной системе координат скорости точки v складывается из скоростей ее поступательного и вращательного движений (см. Рис. 4). По теореме косинусов квадрат модуля скорости равен
\[{\upsilon ^2} = \upsilon _0^2 + \upsilon _0^2 — 2\upsilon _0^2\cos \left( {180^\circ — \alpha } \right) = 2\upsilon _0^2\left( {1 + \cos \alpha } \right).\]
Проекция ускорения точки на направление, перпендикулярное к скорости, равна
\[{a_ \bot } = \frac{{\upsilon _0^2}}{R}\cos \frac{\alpha }{2}.\]
Тогда радиус кривизны траектории точки равен
\[\rho = \frac{{{\upsilon ^2}}}{{{a_ \bot }}} = 4R\cos \frac{\alpha }{2}.\]
Упражнения
- Небольшое тело соскальзывает без трения с поверхности полусферы (см. задачу 3). Определите направление, под которым тело отскочит от горизонтальной плоскости, и максимальную высоту его подъема после отскока. Удар тела о плоскость считайте абсолютно упругим.
- Диск радиусом \(R\), закрученный около своей оси с угловой скоростью \(\omega\), бросают со скоростью \(\overrightarrow \upsilon\) под углом \(\alpha\) к горизонту (рис.5). Определите радиус кривизны траектории точки A диска в момент его максимального подъема. Плоскость диска все время остается вертикальной.
- Автомобиль массой \(m=10^3\) кг начинает двигаться с постоянной тангенциальной проекцией ускорения \(a_т=1\) м/с2 по шоссе в виде дуги окружности радиусом \(R=100\) м. Какую максимальную скорость он наберет до начала проскальзывания колес по асфальту, если коэффициент трения скольжения равен \(\mu=0,3\)? Какую мощность должен развить к этому моменту двигатель автомобиля?
Источник: Журнал “Квант”, №10 1981 г. Автор: А. Шеронов.