Условие задачи:

Пробковый спасательный круг имеет массу 3,2 кг. Определить подъемную силу этого круга в море. Плотность морской воды 1030 кг/м³.

Задача №3.3.19 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m=3,2\) кг, \(\rho_{мв}=1030\) кг/м³, \(F-?\)

Решение задачи:

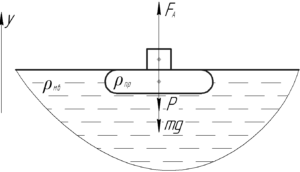Вполне понятно, что подъемная сила спасательного круга \(F\) равна (численно) весу максимального груза \(P\), который этот круг может удерживать, находясь полностью в воде (смотрите схему).

\[F = P\]

Круг будет находиться в равновесии, поэтому можем записать первый закон Ньютона в проекции на ось \(y\):

\[{F_А} = mg + P\]

\[P = {F_А} — mg\]

Или учитывая, что \(F=P\), имеем:

\[F = {F_А} — mg\;\;\;\;(1)\]

Силу Архимеда \(F_А\) будем определять по формуле:

\[{F_А} = \rho _{мв} gV\]

Зная массу спасательного круга, его объем можно определить через плотность пробки (\(\rho_{пр}=200\) кг/м³) по формуле:

\[V = \frac{m}{{{\rho _{пр}}}}\]

Тогда:

\[{F_А} = {\rho _{мв}}g\frac{m}{{{\rho _{пр}}}}\]

Это выражение подставим в формулу (1):

\[F = {\rho _{мв}}g\frac{m}{{{\rho _{пр}}}} — mg\]

\[F = mg\left( {\frac{{{\rho _{мв}}}}{{{\rho _{пр}}}} — 1} \right)\]

Задача решена в общем виде. Посчитаем численный ответ:

\[F = 3,2 \cdot 10 \cdot \left( {\frac{{1030}}{{200}} — 1} \right) = 132,8\;Н\]

Ответ: 132,8 Н.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

3.3.18 Надводная часть айсберга имеет объем 1000 м3. При какой плотности льда объем
3.3.20 Шарик плавает в сосуде, в котором находятся вода и масло. При этом 2/3 объема
3.3.21 Вес тела в воде в 5 раз меньше, чем в воздухе. Какова плотность вещества тела?