Условие задачи:
Катер прошел первую половину пути со скоростью в 2 раза большей, чем вторую. Средняя скорость на всем пути составила 4 км/ч. Какова скорость катера на второй половине пути?
Задача №1.2.9 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(S_1=S_2=\frac{1}{2}S\), \(\upsilon_1=2\upsilon_2\), \(\upsilon_{ср}=4\) км/ч, \(\upsilon_2-?\)
Решение задачи:
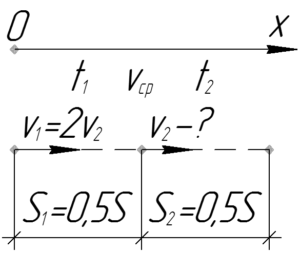Среднюю скорость катера можно сосчитать по формуле:
\[{\upsilon _{ср}} = \frac{{{S_1} + {S_2}}}{{{t_1} + {t_2}}}\]
Движение на обоих участках было равномерным, поэтому найти время \(t_1\) и \(t_2\) не составит труда.
\[\left\{ \begin{gathered}
{t_1} = \frac{{{S_1}}}{{{\upsilon _1}}} \hfill \\
{t_2} = \frac{{{S_2}}}{{{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Так как участки равны по величине \(S_1=S_2=\frac{1}{2}S\), и скорость на первой участке больше скорости на втором в два раза \(\upsilon_1=2\upsilon_2\), то:
\[\left\{ \begin{gathered}
{t_1} = \frac{S}{{2{\upsilon _1}}} = \frac{S}{{4{\upsilon _2}}} \hfill \\
{t_2} = \frac{S}{{2{\upsilon _2}}} \hfill \\
\end{gathered} \right.\]
Подставим выражения для времен \(t_1\) и \(t_2\) в формулу средней скорости.
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{4{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}}}} = \frac{S}{{\frac{{3S}}{{4{\upsilon _2}}}}} = \frac{{S \cdot 4{\upsilon _2}}}{{3S}} = \frac{{4{\upsilon _2}}}{3}\]
Значит необходимая нам скорость \(\upsilon_2\) определяется по такой формуле.
\[{\upsilon _2} = \frac{{3{\upsilon _{ср}}}}{4}\]
Численно же ответ равен:
\[{\upsilon _2} = \frac{{3 \cdot 4}}{4} = 3\; км/ч = 0,83\; м/с\]
Ответ: 0,83 м/с.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
1.2.8 С какой постоянной скоростью должна двигаться нефть в трубопроводе с площадью
1.2.10 Тело первую половину пути двигалось со скоростью 12 км/ч. После этого половину
1.2.11 Первую половину пути велосипедист проехал со скоростью в 8 раз большей, чем
Непонятно почему t2 имеет такой вид. Ведь V1=2V2, а V2=V2, а не 2V2
А что тут непонятного? Время \(t_2\), которое требуется катеру, чтобы пройти половину пути \(\frac{S}{2}\) со скоростью \(\upsilon_2\) легко найти по всем известной формуле:\[{t_2} = \frac{S}{{2{\upsilon _2}}}\]Аналогично для первой половины пути:\[{t_1} = \frac{S}{{2{\upsilon _1}}}\]Так как нам нужно найти \(\upsilon_2\), то в этой последней формуле необходимо заменить \(\upsilon_1\) на \(\upsilon_2\), зная, что \(\upsilon_1 = 2\upsilon_2\). Получим:\[{t_1} = \frac{S}{{2 \cdot 2{\upsilon _2}}} = \frac{S}{{4{\upsilon _2}}}\]
Объясните, пожалуйста, почему 3 км/ч = 0,83 м/с? У меня получилось 10, 8 м/с:
3 км/ч = (3 * 3600) / 1000 м/с = 10800 / 1000 м/с = 10, 8 м/с
\[3\;\frac{км}{ч} = \frac{{3000}}{{3600}}\;\frac{м}{с} = 0,83\;м/с\]
в задаче ведь говорится, что нужно найти скорость катера на второй половине пути. Тогда скорость должна быть равна 3 * 2 = 6 м/с
Я и нашёл скорость на второй половине пути через среднюю скорость
Можете памоч
Катер прошел первую половину пути со скоростью в два раза больше чем вторую.Средняя скорость на всем пути составила 1м/с.Найти скорость катера на первой половине пути
\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{2{\upsilon _1}}} + \frac{S}{{2{\upsilon _2}}}}}\]Так как в Вашем случае \({\upsilon _2} = 0,5{\upsilon _1}\), то:\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{2{\upsilon _1}}} + \frac{S}{{{\upsilon _1}}}}}\]\[{\upsilon _{ср}} = \frac{S}{{\frac{S}{{2{\upsilon _1}}} + \frac{S}{{{\upsilon _1}}}}} = \frac{S}{{\frac{{S + 2S}}{{2{\upsilon _1}}}}} = \frac{{2{\upsilon _1}S}}{{3S}} = \frac{{2{\upsilon _1}}}{3}\]\[{\upsilon _1} = \frac{{3{\upsilon _{ср}}}}{2}\]\[{\upsilon _1} = \frac{{3 \cdot 1}}{2} = 1,5\;м/с\]
У вас Vср из условия задачи в км\ч, а для решения вы уже взяли м\с?)
Нет, я ответ посчитал сначала в км/ч, а затем перевёл в м/с.
Как получилось 3S/4v2 подскажите,пожалуйста?
Сложил две дроби в знаменателе, приведя их под общий знаменатель
Спасибо)
Не 2s? Или вы и числитель добавили как-то?
\[\frac{S}{{4{\upsilon _2}}} + \frac{S}{{2{\upsilon _2}}} = \frac{S}{{4{\upsilon _2}}} + \frac{{2S}}{{4{\upsilon _2}}} = \frac{{3S}}{{4{\upsilon _2}}}\]
Как получилось 4v2/3?
Я не понимаю…
В предыдущей строке получили:
v_ср=4*v_2/3
Откуда:
v_2=3*v_ср/4
Во второй фигурной скобке не совсем понял, почему t1 = S/2V1, можно как-то поподробнее объяснить это?
Читайте объяснение, приведенное выше этой системы:
“Так как участки равны по величине S1=S2=S/2, и скорость на первой участке больше скорости на втором в два раза v1=2v2”
Не понятно откуда взялась формула где v2=3Vcr : 4
Очевидно из рассуждений, приведённых выше этой формулы