Решение: Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона

Условие задачи:

Тело соскальзывает без начальной скорости с наклонной плоскости. Угол наклона плоскости к горизонту 30°, длина плоскости 2 м. Коэффициент трения тела о плоскость 0,3. Каково ускорение тела и сколько длится соскальзывание?

Задача №2.3.8 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(L=2\) м, \(\mu=0,3\), \(a-?\), \(t-?\)

Решение задачи:

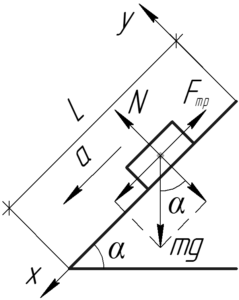Приведем к задаче схему, на которой изобразим наклонную плоскость с телом, а также систему координат. Покажем все силы, действующие на тело: силу тяжести, силу реакции опоры и силу трения скольжения. Так как тело движется ускоренно вдоль оси \(x\), то запишем второй закон Ньютона в проекции на эту ось:

\[mg \cdot \sin \alpha — {F_{тр}} = ma\;\;\;\;(1)\]

По оси \(y\) тело не движется, поэтому второй закон Ньютона в проекции на эту ось запишется в следующем виде:

\[N = mg \cdot \cos \alpha \]

Сила трения скольжения определяется по формуле:

\[{F_{тр}} = \mu N\]

\[{F_{тр}} = \mu mg \cdot \cos \alpha \]

Полученное выражения для \(F_{тр}\) подставим в (1), после чего, сократив обе части на массу \(m\), найдем ответ на первый вопрос задачи.

\[mg \cdot \sin \alpha — \mu mg \cdot \cos \alpha = ma\]

\[a = g\left( {\sin \alpha — \mu \cos \alpha } \right)\;\;\;\;(2)\]

Чтобы найти ответ ко второму вопросу, запишем уравнение движения тела вдоль оси \(x\). Так как тело начинает движение без начальной скорости равноускоренно с ускорением \(a\), то оно примет вид:

\[x = \frac{{a{t^2}}}{2}\]

За искомое время \(t\) тело пройдет расстояние \(L\), поэтому:

\[L = \frac{{a{t^2}}}{2}\]

Откуда:

\[t = \sqrt {\frac{{2L}}{a}} \]

Учитывая (2), эта формула примет вид:

\[t = \sqrt {\frac{{2L}}{{g\left( {\sin \alpha — \mu \cos \alpha } \right)}}} \]

Все данные задачи приведены в системе СИ, поэтому сразу можем приступить к расчету численных ответов.

\[a = 10 \cdot \left( {\sin 30^\circ — 0,3 \cdot \cos 30^\circ } \right) = 2,4\; м/с^2\]

\[t = \sqrt {\frac{{2 \cdot 2}}{{10 \cdot \left( {\sin 30^\circ — 0,3 \cdot \cos 30^\circ } \right)}}} = 1,29\; с\]