Условие задачи:
Тело скользит с постоянной скоростью вниз по наклонной плоскости с углом наклона 45° к горизонту. Определить коэффициент трения.
Задача №2.3.1 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=45^\circ\), \(\mu-?\)
Решение задачи:
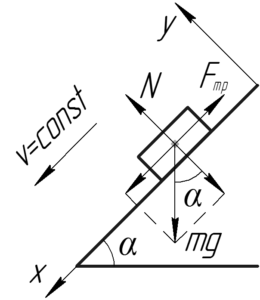На схеме к задаче покажем наклонную плоскость со скользящим по ней телом. Введем оси координат: ось \(y\) перпендикулярно наклонной плоскости, а ось \(x\) – вдоль неё. Покажем все силы, действующие на тело. Так как вдоль оси \(y\) тело не движется, а вдоль оси \(x\) движется равномерно, то запишем первый закон Ньютона в проекции на обе оси:
\[\left\{ \begin{gathered}
N = mg \cdot \cos \alpha \;\;\;\;(1)\hfill \\
mg \cdot \sin \alpha = {F_{тр}} \;\;\;\;(2)\hfill \\
\end{gathered} \right.\]
Сила трения скольжения определяется по формуле:
\[{F_{тр}} = \mu N\]
Учитывая (1), имеем:
\[{F_{тр}} = \mu mg \cdot \cos \alpha \]
Подставим полученное выражение для силы трения в (2), тогда:
\[mg \cdot \sin \alpha = \mu mg \cdot \cos \alpha \]
\[\mu = tg\alpha \]
Посчитаем численное значение коэффициента трения:
\[\mu = tg45^\circ = 1\]
Ответ: 1.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.2.9 К одному концу невесомой и нерастяжимой нити, перекинутой через невесомый блок
2.3.2 Льдинка скользит по инерции вверх по наклонной плоскости с углом наклона
2.3.3 По канатной дороге, идущей с уклоном 30 градусов к горизонту, опускается вагонетка
А там разве не котангенс получается ?
Нееет. Мы получили следующее: \[mg \cdot sin\alpha = \mu mg \cdot cos\alpha \] Обе части этого уравнения делим на \(mg \cdot cos\alpha \), тогда получим: \[\mu = tg\alpha \]
кстати можно просто выразить мю и тогда мы сократим мж и останеться всего лишь синус на косинус и получиться 1
А если есть еще и вертикальная сила, как вот в этой задаче: “Брусок массой 2 кг, к которому приложена сила 4 Н, направленная вертикально вверх, равномерно движется вниз по шероховатой наклонной плоскости с углом при основании 30°. Чему равен модуль работы, которую совершит над бруском сила трения при перемещении бруска на 1 м?”
Вам нужно при записи первого закона Ньютона также спроецировать силу \(F\) (которая равна 4 Н). Вы должны получить следующее:
\[\left\{ \begin{gathered}
N + F\cos \alpha = mg\cos \alpha \hfill \\
mg\sin \alpha = F\sin \alpha + {F_{тр}} \hfill \\
\end{gathered} \right.\]Отсюда выражаете силу реакции опоры \(N\), а далее находите силу трения \(F_{тр}\) и её работу.
\[N = \left( {mg – F} \right)\cos \alpha \]\[{F_{тр}} = \mu N = \mu \left( {mg – F} \right)\cos \alpha \]\[A = {F_{тр}}S = \mu \left( {mg – F} \right)S\cos \alpha \]