Условие задачи:
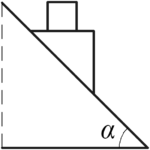 По наклонной плоскости с углом наклона 60° соскальзывает без трения клин. На верхней поверхности горизонтальной грани клина лежит груз массой 0,4 кг, неподвижный относительно клина. Найти силу трения покоя, действующую на груз.
По наклонной плоскости с углом наклона 60° соскальзывает без трения клин. На верхней поверхности горизонтальной грани клина лежит груз массой 0,4 кг, неподвижный относительно клина. Найти силу трения покоя, действующую на груз.
Задача №2.3.20 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(\alpha=60^\circ\), \(m=0,4\) кг, \(F_{тр}-?\)
Решение задачи:
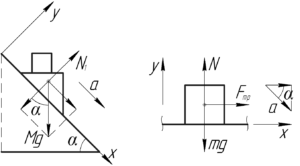 Введем на данной к задаче схеме систему координат: \(y\) перпендикулярно наклонной плоскости, а \(x\) вдоль неё. Рассмотрим систему «клин — груз». Так как клин движется без трения, то на эту систему действует две внешние силы: сила тяжести и сила реакции опоры. Запишем теорему о движении центра масс в проекции на ось \(x\):
Введем на данной к задаче схеме систему координат: \(y\) перпендикулярно наклонной плоскости, а \(x\) вдоль неё. Рассмотрим систему «клин — груз». Так как клин движется без трения, то на эту систему действует две внешние силы: сила тяжести и сила реакции опоры. Запишем теорему о движении центра масс в проекции на ось \(x\):
\[Mg \cdot \sin \alpha = Ma\]
Здесь \(M\) — это масса системы, т.е. суммарная масса клина с грузом. Так как совместное движение клина с грузом является поступательным, а вращательное движение отсутствует, значит каждая точка этой системы движется с этим ускорением:
\[a = g \cdot \sin \alpha \;\;\;\;(1)\]
Теперь рассмотрим груз. Для этого введем оси координат, как показано на схеме справа. На груз действуют три силы: сила тяжести, сила реакции опоры и сила трения покоя (обратите внимание на её направление). При этом груз движется ускоренно с ускорением \(a\) относительно Земли. Применим второй закон Ньютона в проекции на ось \(x\):
\[{F_{тр}} = ma \cdot \cos \alpha \]
Используя ранее найденное выражение для ускорения (1), имеем:
\[{F_{тр}} = mg \cdot \sin \alpha \cdot \cos \alpha \]
\[{F_{тр}} = \frac{{mg \cdot \sin 2\alpha }}{2}\]
Так как все численные величины даны в системе СИ, то можем сразу посчитать ответ:
\[{F_{тр}} = \frac{{0,4 \cdot 10 \cdot \sin 120^\circ }}{2} = 1,73\; Н\]
Ответ: 1,73 Н.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень
2.3.21 Груз поднимают с помощью ленточного транспортера, расположенного под углом
2.3.22 На горизонтальной доске лежит брусок. Коэффициент трения скольжения между бруском
А почему трение направлено именно вправо?
Сила трения направлена против проскальзывания, брусок мог проскользнуть только вправо