Два тела масс m1 и m2, связанные невесомой нитью, лежат на гладкой горизонтальной

Условие задачи:

Два тела масс \(m_1\) и \(m_2\), связанные невесомой нитью, лежат на гладкой горизонтальной поверхности. Нить обрывается, если сила её натяжения превышает значение \(T_m\). C какой максимальной горизонтальной силой \(F\) можно тянуть второе тело, чтобы нить не оборвалась?

Задача №2.1.82 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(m_1\), \(m_2\), \(T_m\), \(F_m-?\)

Решение задачи:

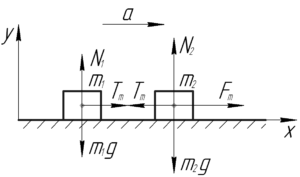Потянем второе тело с такой силой \(F_m\), что сила натяжения нити, соединяющей тела, станет очень близка по величине к \(T_m\), но ещё не разорвется.

По условию поверхность, по которой движутся тела, гладкая, значит сил трения нет. Покажем на схеме все силы, действующие на тела, потом запишем второй закон Ньютона для обоих тел в проекции на ось \(x\). Ускорения рассматриваемых тел, естественно, одинаковые.

\[\left\{ \begin{gathered}
{F_m} – {T_m} = {m_2}a \hfill \\
{T_m} = {m_1}a \hfill \\
\end{gathered} \right.\]

Сложим оба выражения системы, а из полученного выразим ускорение \(a\).

\[{F_m} = \left( {{m_1} + {m_2}} \right)a\]

\[a = \frac{{{F_m}}}{{{m_1} + {m_2}}}\]

Подставим формулу в последнее выражение системы, а оттуда выразим искомую силу \(F_m\).

\[{T_m} = \frac{{{F_m}{m_1}}}{{{m_1} + {m_2}}}\]

\[{F_m} = \frac{{{T_m}\left( {{m_1} + {m_2}} \right)}}{{{m_1}}}\]

Поделим почленно числитель дроби на знаменатель.

\[{F_m} = {T_m}\left( {1 + \frac{{{m_2}}}{{{m_1}}}} \right)\]

В условии не было дано числовых данных, задачу требовалось решить в общем виде, что мы и сделали.

Ответ: \({T_m}\left( {1 + \frac{{{m_2}}}{{{m_1}}}} \right)\).

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.1.81 Четыре одинаковых кубика, связанные невесомыми нитями, движутся по гладкому
2.1.83 Стержень длины L движется по гладкой горизонтальной поверхности. Какая упругая
2.1.84 Тело массы 10 кг движется по горизонтальной плоскости под действием силы