Условие задачи:

Чему должен быть равен минимальный коэффициент трения между шинами и поверхностью наклонной дороги с уклоном 30°, чтобы автомобиль мог двигаться по ней вверх с ускорением 0,6 м/с²?

Задача №2.3.17 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\alpha=30^\circ\), \(a=0,6\) м/с², \(\mu-?\)

Решение задачи:

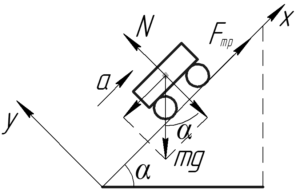Схематично изобразим автомобиль на наклонной дороге, введем систему координат и покажем все силы, действующие на автомобиль. На него действует сила тяжести, сила реакции опоры (на рисунке изображена суммарная со стороны двух колес) и сила трения покоя (которая равна силе тяги автомобиля).

Обратите внимание, что между шинами и дорогами действует именно сила трения покоя, иначе автомобиль бы проскальзывал. Причем чтобы соблюсти условие минимальности коэффициента трения, эта сила трения покоя должна принять максимальное значение, т.е. быть равной силе трения скольжения, хотя автомобиль ещё не проскальзывает. Сила трения направлена вверх, поскольку автомобиль стремится соскользнуть вниз.

Запишем второй закон Ньютона в проекции на ось \(x\):

\[{F_{тр}} — mg \cdot \sin \alpha  = ma\;\;\;\;(1)\]

Так как автомобиль покоится вдоль оси \(y\), то применим первый закон Ньютона в проекции на эту ось:

\[N = mg \cdot \cos \alpha \;\;\;\;(2)\]

Силу трения покоя найдем по формуле (смотри объяснения выше):

\[{F_{тр}} = \mu N\]

Учитывая (2), имеем:

\[{F_{тр}} = \mu mg \cdot \cos \alpha \]

Подставим полученное в равенство (1):

\[\mu mg \cdot \cos \alpha  — mg \cdot \sin \alpha  = ma\]

Осталось только выразить коэффициент \(\mu\), что мы сейчас и сделаем:

\[\mu  = \frac{{a + g \cdot \sin \alpha }}{{g \cdot \cos \alpha }}\]

Посчитаем ответ:

\[\mu  = \frac{{0,6 + 10 \cdot \sin 30^\circ }}{{10 \cdot \cos 30^\circ }} = 0,65\]

Ответ: 0,65.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

2.3.16 С горы высотой 2 м и основанием 5 м съезжают санки, которые затем останавливаются
2.3.18 Два бруска одинаковой массы 0,2 кг поставили на наклонную плоскость с углом
2.3.19 На тележке, скатывающейся без трения с наклонной плоскости, установлен стержень