Условие задачи:

Один моль одноатомного газа совершает цикл, состоящий из двух изохор и двух изобар. При этом максимальное давление в 2 раза больше минимального, а максимальный объем в 3 раза больше минимального. Определите коэффициент полезного действия цикла.

Задача №5.5.45 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=1\) моль, \(p_2=2p_1\), \(V_2=3V_1\), \(\eta-?\)

Решение задачи:

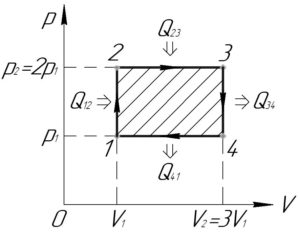Изобразим цикл, совершаемый над газом, в координатах p-V (смотрите схему).

КПД цикла \(\eta\) определяют по формуле:

\[\eta = \frac{A}{{{Q_н}}}\;\;\;\;(1)\]

Работа газа в цикле \(A\) равна площади цикла в координатах p-V, при этом если цикл обходится по часовой стрелке (как у нас), то работа цикла положительна.

\[A = \left( {{p_2} — {p_1}} \right)\left( {{V_2} — {V_1}} \right)\]

Так как по условию \(p_2=2p_1\) и \(V_2=3V_1\), то:

\[A = \left( {2{p_1} — {p_1}} \right)\left( {3{V_1} — {V_1}} \right) = 2{p_1}{V_1}\;\;\;\;(2)\]

Отлично! Теперь, чтобы найти количество теплоты \(Q_н\), нужно определить все процессы в цикле, в которых тепло подводилось к газу. Для начала запишем первый закон термодинамики, мы к нему будем постоянно обращаться:

\[Q = \Delta U + A\;\;\;\;(3)\]

Изменение внутренней энергии одноатомного идеального газа \(\Delta U\) определяют по формуле:

\[\Delta U = \frac{3}{2}\nu R\Delta T\;\;\;\;(4)\]

Работу газа \(A\) можно определить следующим образом:

\[A = p\Delta V\;\;\;\;(5)\]

Также запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1-4. В уравнениях сразу учтём, что \(p_2=2p_1\) и \(V_2=3V_1\).

\[\left\{ \begin{gathered}
{p_1}{V_1} = \nu R{T_1} \;\;\;\;(6)\hfill \\
2{p_1}{V_1} = \nu R{T_2} \;\;\;\;(7)\hfill \\
2{p_1} \cdot 3{V_1} = \nu R{T_3} \;\;\;\;(8)\hfill \\
{p_1} \cdot 3{V_1} = \nu R{T_4} \hfill \\
\end{gathered} \right.\]

Рассмотрим процесс 1-2, который является изохорным (\(V=const\)), значит работа газа \(A_{12}\) в этом процессе равна нулю (так как \(\Delta V_{12}=0\)). Поэтому количество теплоты \(Q_{12}\) по формуле (3) равно:

\[{Q_{12}} = \Delta {U_{12}}\]

Тогда согласно формуле (4), имеем:

\[{Q_{12}} = \frac{3}{2}\nu R\Delta {T_{12}}\;\;\;\;(9)\]

Так как в этом изохорном процессе давление увеличивается, значит по закону Шарля температура также растёт (\(\Delta T_{12}>0\)). Поэтому из формулы (9) следует, что тепло в процессе 1-2 подводилось (\(Q_{12}>0\)). Отнимем из уравнения (7) уравнение (6):

\[{p_1}{V_1} = \nu R\left( {{T_2} — {T_1}} \right)\]

\[{p_1}{V_1} = \nu R\Delta {T_{12}}\]

Тогда формула (9) примет такой вид:

\[{Q_{12}} = \frac{3}{2}{p_1}{V_1}\;\;\;\;(10)\]

Если провести аналогичные рассуждения для изохорного процесса 3-4, то Вы выясните, что \(Q_{34}<0\), то есть тепло в этом процессе отводилось от газа.

Также рассмотрим изобарный процесс 2-3 (\(p=const\)). Количество теплоты \(Q_{12}\) согласно формуле (3) равно:

\[{Q_{23}} = \Delta {U_{23}} + {A_{23}}\;\;\;\;(11)\]

Изменение внутренней энергии \(\Delta U_{23}\) по формуле (4) равно:

\[\Delta {U_{23}} = \frac{3}{2}\nu R\Delta {T_{23}}\;\;\;\;(12)\]

Работа газа \(A_{23}\) согласно формуле (5) равна:

\[{A_{23}} = {p_2} \cdot \left( {{V_2} — {V_1}} \right) = {p_2}{V_2} — {p_2}{V_1}\]

Так как в условии сказано, что \(p_2=2p_1\) и \(V_2=3V_1\), то:

\[{A_{23}} = 2{p_1} \cdot 3{V_1} — 2{p_1}{V_1}\]

Учитывая уравнения (7) и (8), имеем:

\[{A_{23}} = \nu R{T_3} — \nu R{T_2}\]

\[{A_{23}} = \nu R\Delta {T_{23}}\;\;\;\;(13)\]

Подставив выражения (12) и (13) в формулу (11), получим:

\[{Q_{23}} = \frac{3}{2}\nu R\Delta {T_{23}} + \nu R\Delta {T_{23}}\]

\[{Q_{23}} = \frac{5}{2}\nu R\Delta {T_{23}}\;\;\;\;(14)\]

Так как в изобарном процессе 2-3 объем увеличивался, значит по закону Гей-Люссака его температура росла (\(\Delta T_{23}>0\)). Поэтому из формулы (14) следует, что тепло в процессе 2-3 подводилось (\(Q_{23}>0\)). Отнимем из уравнения (8) уравнение (7):

\[4{p_1}{V_1} = \nu R\left( {{T_3} — {T_2}} \right)\]

\[4{p_1}{V_1} = \nu R\Delta {T_{23}}\]

Тогда формула (14) примет такой вид:

\[{Q_{23}} = \frac{5}{2} \cdot 4{p_1}{V_1}\]

\[{Q_{23}} = 10{p_1}{V_1}\;\;\;\;(15)\]

Проведя аналогичные рассуждения для изобарного процесса 4-1, Вы выясните, что \(Q_{41}<0\), то есть тепло в этом процессе отводилось от газа.

В ходе наших рассуждений мы выяснили, что к газу теплота подводится только в процессах 1-2 и 2-3, то есть количество теплоты \(Q_н\) равно:

\[{Q_н} = {Q_{12}} + {Q_{23}}\]

Примем во внимание полученные равенства (10) и (15), тогда:

\[{Q_н} = \frac{3}{2}{p_1}{V_1} + 10{p_1}{V_1}\]

\[{Q_н} = \frac{{23}}{2}{p_1}{V_1}\;\;\;\;(16)\]

Тогда согласно формуле (1) коэффициент полезного действия цикла \(\eta\), учитывая выражения (2) и (16), равен:

\[\eta = \frac{{2{p_1}{V_1}}}{{\frac{{23}}{2}{p_1}{V_1}}} = \frac{4}{{23}} = 0,174\]

Ответ: 0,174.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Смотрите также задачи:

5.5.44 Тепловая машина с максимально возможным КПД имеет в качестве нагревателя
5.5.46 Над одним молем идеального газа совершают цикл, показанный на рисунке
5.5.47 В некотором процессе внутренняя энергия газа уменьшилась на 300 Дж, а газ