Решение: Некоторая масса газа, занимающего объем 0,01 м3, находится при давлении 0,1 МПа

Условие задачи:

Некоторая масса газа, занимающего объем 0,01 м³, находится при давлении 0,1 МПа и температуре 300 К. Газ нагревается вначале при постоянном объеме до 320 К, а затем при постоянном давлении до 350 К. Найти работу, совершаемую газом при переходе из начального состояния в конечное.

Задача №5.4.28 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(V_1=0,01\) м³, \(p_1=0,1\) МПа, \(T_1=300\) К, \(T_2=320\) К, \(T_3=350\) К, \(A-?\)

Решение задачи:

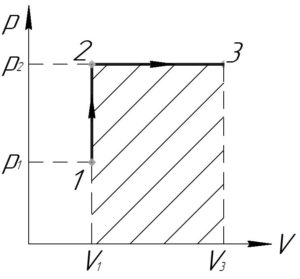Изобразим происходящие над газом процессы в координатах p-V (смотрите схему).

Суммарная работа газа \(A\) равна сумме работ газа в процессах 1-2 и 2-3:

\[A = {A_{12}} + {A_{23}}\]

Как сказано в условии, первый процесс 1-2 является изохорным (\(V=const\)), работа газа при изохорном процессе \(A_{12}\) равна нулю, так как объем газа не изменяется.

\[{A_{12}} = 0\]

Поэтому суммарная работа газа \(A\) равна работе газа в процессе 2-3:

\[A = {A_{23}}\;\;\;\;(1)\]

Процесс 2-3 — изобарный (\(p=const\)), при этом температура газа увеличивается, а значит по закону Гей-Люссака растёт и объём газа. Работу газа при изобарном расширении \(A_{23}\) найдём по известной формуле:

\[{A_{23}} = {p_2}\left( {{V_3} — {V_1}} \right) = {p_2}{V_3} — {p_2}{V_1}\;\;\;\;(2)\]

Численно эта работа равна площади фигуры под графиком процесса 1-2 (на схеме к решению — заштриховано).

Запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1, 2 и 3:

\[\left\{ \begin{gathered}
{p_1}{V_1} = \nu R{T_1} \;\;\;\;(3)\hfill \\
{p_2}{V_1} = \nu R{T_2} \;\;\;\;(4)\hfill \\
{p_2}{V_3} = \nu R{T_3} \;\;\;\;(5)\hfill \\
\end{gathered} \right.\]

Учитывая уравнения (4) и (5), формула (2) примет вид:

\[{A_{23}} = \nu R{T_3} — \nu R{T_2} = \nu R\left( {{T_3} — {T_2}} \right)\;\;\;\;(6)\]

Из уравнения (3) выразим количество вещества \(\nu\):

\[\nu = \frac{{{p_1}{V_1}}}{{R{T_1}}}\]

Полученное выражение подставим в формулу (6), тогда:

\[{A_{23}} = \frac{{{p_1}{V_1}}}{{R{T_1}}}R\left( {{T_3} — {T_2}} \right)\]

\[{A_{23}} = \frac{{{p_1}{V_1}}}{{{T_1}}}\left( {{T_3} — {T_2}} \right)\]

С учётом равенства (1) имеем:

\[A = \frac{{{p_1}{V_1}}}{{{T_1}}}\left( {{T_3} — {T_2}} \right)\]

Подставим все значения величин в формулу и посчитаем численный ответ задачи:

\[A = \frac{{0,1 \cdot {{10}^6} \cdot 0,01}}{{300}} \cdot \left( {350 — 320} \right) = 100\;Дж = 0,1\;кДж\]