Условие задачи:
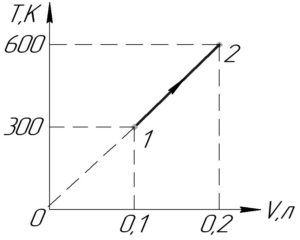
На диаграмме T (температура) — V (объем) график процесса представляет собой прямую, соединяющую точки (300 К; 0,1 л), (600 К; 0,2 л). Определить работу одного моля идеального газа при расширении от 0,1 до 0,2 л.
Задача №5.4.26 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»
Дано:
\(T_1=300\) К, \(V_1=0,1\) л, \(T_2=600\) К, \(V_2=0,2\) л, \(\nu=1\) моль, \(A-?\)
Решение задачи:
 Легко заметить, что отношение объема газа к температуре всегда остаётся постоянным:
Легко заметить, что отношение объема газа к температуре всегда остаётся постоянным:
\[\frac{{{V_1}}}{{{T_1}}} = \frac{{{V_2}}}{{{T_2}}}\]
Переведём объемы газа в систему СИ:
\[0,1\;л = 0,1 \cdot {10^{ — 3}}\;м^3\]
\[0,2\;л = 0,2 \cdot {10^{ — 3}}\;м^3\]
Тогда:
\[\frac{{0,1 \cdot {{10}^{ — 3}}}}{{300}} = \frac{{0,2 \cdot {{10}^{ — 3}}}}{{600}} = 3,33 \cdot {10^{ — 7}}\]
Указанное равенство является законом Гей-Люссака, значит процесс 1-2 является изобарным (\(p=const\)). Кстати, это также означает, что продолжение графика процесса 1-2 попадёт в начало координат (смотрите схему к решению).
Работу идеального газа при изобарном расширении \(A\) находят таким образом:
\[A = p\left( {{V_2} — {V_1}} \right) = p{V_2} — p{V_1}\;\;\;\;(1)\]
Запишем уравнение Клапейрона-Менделеева для состояния газа в точках 1 и 2:
\[\left\{ \begin{gathered}
p{V_1} = \nu R{T_1} \hfill \\
p{V_2} = \nu R{T_2} \hfill \\
\end{gathered} \right.\]
Тогда формула (1) станет такой:
\[A = \nu R{T_2} — \nu R{T_1} = \nu R\left( {{T_2} — {T_1}} \right)\]
Задача решена в общем виде. Произведём расчёт численного ответа:
\[A = 1 \cdot 8,31 \cdot \left( {600 — 300} \right) = 2493\;Дж = 2,49\;кДж\]
Ответ: 2,49 кДж.
Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.
Смотрите также задачи:
5.4.25 В цилиндре под тяжелым поршнем находится 20 г углекислого газа. Газ нагревается
5.4.27 Над идеальным газом проводят два замкнутых процесса. Какое соотношение
5.4.28 Некоторая масса газа, занимающего объем 0,01 м3, находится при давлении 0,1 МПа