Решение: Идеальный одноатомный газ в количестве 5 моль сначала охлаждают

Условие задачи:

Идеальный одноатомный газ в количестве 5 моль сначала охлаждают при постоянном объеме от температуры 600 К до температуры 400 К, а затем продолжают охлаждать при постоянном давлении до температуры 300 К. Какое количество теплоты отводят при этом от газа?

Задача №5.5.23 из «Сборника задач для подготовки к вступительным экзаменам по физике УГНТУ»

Дано:

\(\nu=5\) моль, \(T_1=600\) К, \(T_2=400\) К, \(T_3=300\) К, \(Q-?\)

Решение задачи:

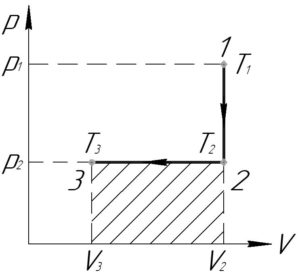На схеме показан график производимых над газом процессов в координатах p-V.

В общем случае первый закон термодинамики гласит, что количество теплоты \(Q\), подведённое к газу, расходуется на изменение внутренней энергии газа \(\Delta U\) и на совершение газом работы \(A\).

\[Q = \Delta U + A\;\;\;\;(1)\]

Процесс 1-2 — изохорный (\(V=const\)), работа газа в этом процессе \(A_{12}\) равна нулю. Изменение внутренней энергии \(\Delta U_{12}\) легко найти по формуле:

\[\Delta {U_{12}} = \frac{3}{2}\nu R\left( {{T_2} — {T_1}} \right)\]

Тогда количество теплоты \(Q_{12}\) согласно формуле (1) можно найти так:

\[{Q_{12}} = \frac{3}{2}\nu R\left( {{T_2} — {T_1}} \right)\]

Процесс 2-3 — изобарный (\(p=const\)). Изменение внутренней энергии \(\Delta U_{23}\) найдём аналогично по формуле:

\[\Delta {U_{23}} = \frac{3}{2}\nu R\left( {{T_3} — {T_2}} \right)\]

Работу газа \(A_{23}\) в изобарном процессе определяют так:

\[{A_{23}} = {p_2}\left( {{V_3} — {V_2}} \right) = {p_2}{V_3} — {p_2}{V_2}\]

Интересно, что абсолютное значение этого выражения численно равно площади фигуры под графиком 2-3 (на схеме заштриховано).

Запишем уравнение Клапейрона-Менделеева для состояния газа в точках 2 и 3:

\[\left\{ \begin{gathered}
{p_2}{V_2} = \nu R{T_2} \hfill \\
{p_2}{V_3} = \nu R{T_3} \hfill \\
\end{gathered} \right.\]

Тогда имеем:

\[{A_{23}} = \nu R{T_3} — \nu R{T_2} = \nu R\left( {{T_3} — {T_2}} \right)\]

Количество теплоты \(Q_{23}\) согласно формуле (1) можно определить следующим образом:

\[{Q_{23}} = \frac{3}{2}\nu R\left( {{T_3} — {T_2}} \right) + \nu R\left( {{T_3} — {T_2}} \right)\]

\[{Q_{23}} = \frac{5}{2}\nu R\left( {{T_3} — {T_2}} \right)\]

Искомое количество теплоты \(Q\) равно сумме количеств теплоты в каждом из процессов, то есть:

\[Q = {Q_{12}} + {Q_{23}}\]

Тогда:

\[Q = \frac{3}{2}\nu R\left( {{T_2} — {T_1}} \right) + \frac{5}{2}\nu R\left( {{T_3} — {T_2}} \right)\]

\[Q = \frac{1}{2}\nu R\left( {3{T_2} — 3{T_1} + 5{T_3} — 5{T_2}} \right)\]

\[Q = \frac{1}{2}\nu R\left( {5{T_3} — 2{T_2} — 3{T_1}} \right)\]

Посчитаем ответ:

\[Q = \frac{1}{2} \cdot 5 \cdot 8,31 \cdot \left( {5 \cdot 300 — 2 \cdot 400 — 3 \cdot 600} \right) = — 22853\;Дж \approx — 23\;кДж\]

Знак «минус» означает, что теплота отводилась от газа. В ответе запишем абсолютное значение, так как спрашивается «какое количество теплоты отводят от газа».